Hey everyone, I appeared for the contest and solved 1972C. I made a stupid error that got me lagging behind int the contest but I found a solution in time. I'm pretty sure, other people might have also come up with this idea but my version makes it easier for beginners to understand.
You can refer to my solution here .
First things first, we start with making maximum number of permutations that we can. We maintain the count of used coins and deduct them whenever used, we break the loop when we reach a point where we have insufficient coins.
sort the array
// ct1 is the number of type of coins passed until now
int ct=a[0],ct1=1;;
for (int i=1;i<n;i++){
if(a[i]>a[i-1]){
int add = ct1*(a[i]-a[i-1]);
if(m<add){
ct+=m/ct1;
m-=(m/ct1)*ct1;
break;
}
else{
ct+=a[i]-a[i-1];
m-=add;
}
}
ct1++;
}
The array a has to be sorted for this to be possible. At the end we will be left with
m : number of coins left (after making all the purchases)
ct : number of permutations we made (full permutations with n elements)
As we are sure that the every permutation we made will require one occurance of every type of card, i.e., 1..n. This implies [ct] permutations will require [ct] occurances of every type of card.
Now we just subtract ct from the available coins, and get the extra coins that we are left with, we will only get 3 cases for each type of coin viz, [no coins left], [one coin left] and [more than or equal to two coins left].
Lets store number of type of coins that appear once and more than once in n1 and n2 variables respectively.
int n2=0,n1=0;
for(int i=0;i<n;i++){
k=max((int)0,k-ct);
if(k>=2){
n2++;
}
else if(k>=1){
n1++;
}
}
We only have to consider the number of permutations possible. We already made ct permutations.
That would fetch us the answer ct*n-(n-1) . As when arranged, we can start from any index except the last n-1 indices to count our permutations (look the image below). lets call this number to be ans.
ans = ct*n-(n-1)
Example: 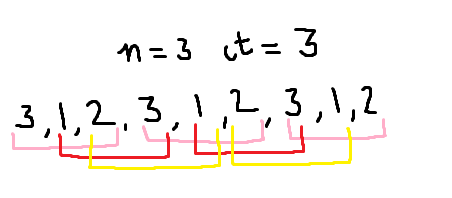
Now simply for a fact we can say that m + n2 + n1 will not exceed n (as that would mean we have not considered a possible permutation).
Now we only have to address the n2 and n1 count. Since we already know that [n2 + n1 + m] will not exceed n, we can add it directly to the answer.
**This is an alternative way to think, not a part of solution **
We can address the n2 count particularly this way:
add n2 elements in the front and back of already made permutations, on top of that, if we have more coins left, we can add m/2 elements to front and back as well. that would lead our solution to be max of ans and [ (_m_/2 + n2)*2+ans ].
We can visualize it as follows : We already have at least one instances of [n1+n2] different types of cards, we can buy m more, since we are left with m coins. Hence the answer.
I made this blog because I thought I found a O (n) solution but later realized i sorted the array in the beginning, poor me.






