Hello everyone. Today I would like to introduce you to a new technique — ternary search on non-unimodal functions. I came up with it during ROI 2024 and it helped me to become a prize winner.
The motivation
There are many examples in CP where we need to maximise or minimise the value of some function $$$f$$$. If the function is unimodal, there is no problem using ternary search. But if it's not, there's nothing to do. Of course, if $$$f$$$ is random, we should check all its values. Fortunately, intuition tells us that if the function is often close to unimodal, we can also use ternary search on a large part of its area of definition.
The intuition
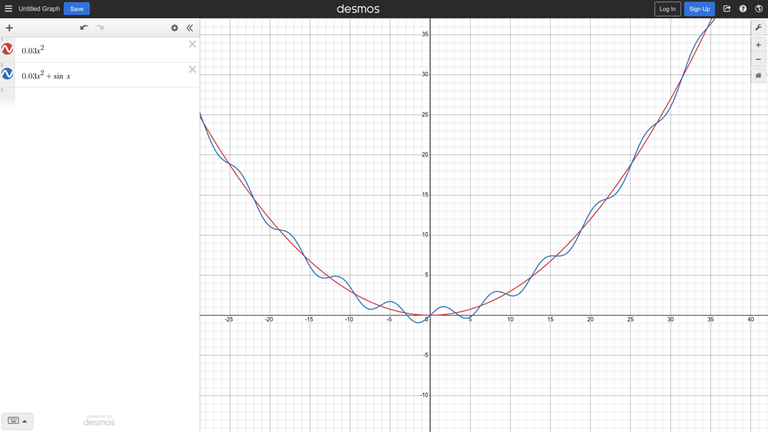
Consider the unimodal function $$$0.03x^2$$$ after adding some noise ($$$sin (x)$$$) to it:
Intuition suggests that if the noise is not strong, we can still use a ternary search away from the global minimum.
In this example, we can put it more formally — the derivative of the function is $$$0.06x + cos(x)$$$, and when $$$|x| > \frac{1}{0.06} \approx 16.67$$$, adding cosine does not change the sign of the derivative.
The first optimisation
So, the first idea is to run the ternary search using not while (r - l > eps) but while (r - l > C) and then bruteforce all values between $$$l$$$ and $$$r$$$ with some precision. In many cases when $$$f$$$ takes an integer argument there will be no precision issue at all.
The second optimisation
It is mentioned in this blog. It tells us a similar idea of splitting all argument values into blocks and applying ternary search on them.
This is the only thing related to the blog that I found. I tried googling and asking people involved in CP, but none of them knew about it before.
Testing
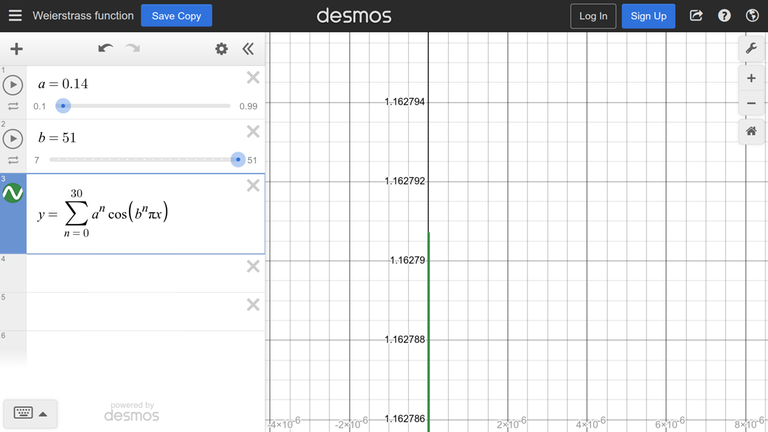
The function from the example is boring, so consider a more interesting function: Weierstrass function
We zoom in and find that the maximum is about $$$1.162791$$$
We will search for the maximum on the interval (-1, 1).
This gives us $$$1.12881$$$. Changing $$$eps$$$ will change this value slightly.
Let's split the arguments into blocks. Since the arguments are real, we will not actually split them explicitly into blocks, we will take the maximum in some range near the argument.
It gives $$$1.15616$$$, which is quite good. We can optimise it by taking the maximum of all the values of $$$f$$$ we have ever calculated:
This gives us $$$1.16278$$$, which is very close to the expected $$$1.162791$$$. It seems that we have found a good approach. But let's go further.
The third optimisation
Let's change the constant $$$3$$$ in the code. We will call it $$$C$$$. It is not new to experienced people, often it is good to choose $$$C$$$ equal to $$$2$$$ (binary search by the derivative) or $$$\frac{\sqrt5+1}{2}$$$ (golden ratio). As we are cutting out $$$\frac{1}{C}$$$ part of our interval on each iteration, the probability of the maximum being indise the cut-off part decreases as C increases.
Let's choose $$$C = 100$$$ and run ternary search. As we already know, taking maximum of all function calls is very good optimisation, so I have already added it.
If we run it with $$$C = 3$$$, we get $$$1.13140$$$ (the algo is the same as the classic ternary search, but we take the maximum, so the answer is much better). Now let's now increase $$$C$$$ and watch the answer increases:
We run it with $$$C = 30$$$ and get $$$1.16275$$$. We run it with $$$C = 100$$$ and get ... $$$1.15444$$$
In fact, increasing $$$C$$$ does not guarantee a better answer.
The fourth optimisation
Let's bruteforce all values of $$$C$$$ from 3 to 100 and take the best answer:
for (int C = 3; C < 100; C++) res = max(res, find_maximum(Weierstrass, C));
It gives us $$$1.16279$$$ and works faster than block splitting. To compare them further, we need to change the function, because both methods return values that are very close to the answer.
Let's use $$$a = 0.88$$$ and $$$b = 51$$$ for the Weierstrass function. Note that it is impossible to see the actual maximum of the function in Desmos.
I will compare the above 2 approaches on Codeforces Custom test.
I tried combining these methods together, but is performs worse than both techniques (because I used $$$1000$$$ iterations instead of $$$10000$$$ and bruteforced $$$C < 10$$$ not to run out of time).
Conclusion
On the function I considered, both approaches are good enough. On real contests I only used my approach.
From recent problems, 2035E - Monster, I have used this technique successfully. Here is the implementation for integer arguments: 288346163.
If you know how to find the maximum better (not by simulated annealing), please write.