Всем привет! Сегодня я хочу познакомить вас с новым алгоритмом: тернарным поиском на неунимодальных функциях. Я придумал ее во время ROI 2024, и благодаря этому стал призером.
Мотивация
В олпроге есть много примеров, когда нам нужно максимизировать или минимизировать значение некоторой функции $$$f$$$. Если функция унимодальна, то нет проблем с использованием тернарного поиска. Но если это неправда, то делать нечего. Конечно, если $$$f$$$ случайна, нужно проверить все ее значения. К счастью, интуиция подсказывает нам, что если функция близка к унимодальной, то мы можем использовать тернарный поиск и на большей части ее области определения.
Интуиция
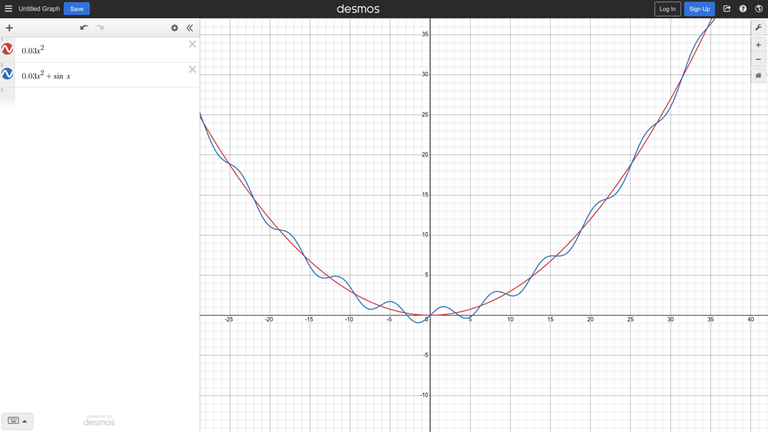
Рассмотрим унимодальную функцию $$$0.03x^2$$$, добавив к ней немного шума ($$$sin (x)$$$):
Интуиция подсказывает, что если шум не очень сильный, мы все равно можем использовать троичный поиск вдали от глобального минимума.
В данном примере мы можем показать это более формально: производная функции равна $$$0.06x + cos(x)$$$, и при $$$|x| > \frac{1}{0.06} \approx 16.67$$$, добавление косинуса не меняет знак производной.
Первая оптимизация
Итак, первая идея — запустить тернарный поиск, используя не while (r - l > eps), а while (r - l > C), и затем перебрать все значения между $$$l$$$ и $$$r$$$ с некоторой точностью. В случае, когда $$$f$$$ принимает целое число, проблема точности вообще отсутствует.
Вторая оптимизация
Она упоминается в этом блоге. В нем рассказывается аналогичная идея разбиения всех значений аргументов на блоки и применения к ним троичного поиска.
Это единственная связанная с блогом идея, которую я нашел в Интернете. Я пробовал гуглить и спрашивать людей, занимающихся олпрогой, но никто из них не знал об этом раньше.
Тесты
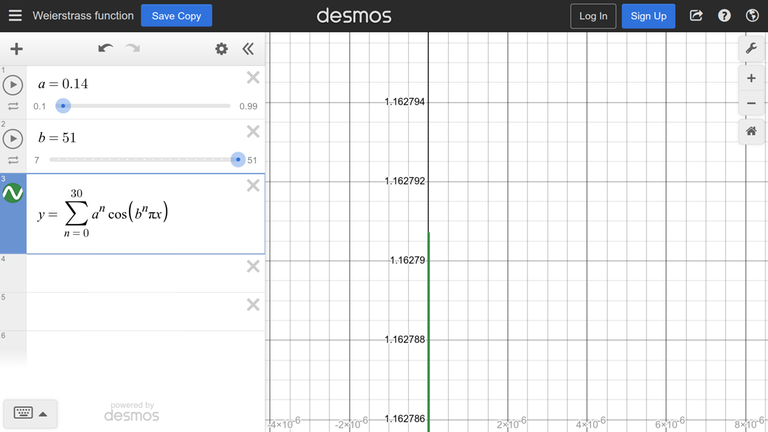
Функция из примера скучна, поэтому рассмотрим более интересную: функция Вейерштрасса.
Приближая, я выяснил, что максимум составляет около $$$1,162791$$$.
Будем искать максимум на интервале (-1, 1).
Это дает нам $$$1,12881$$$. Изменение $$$eps$$$ лишь немного меняет это значение.
Давайте разделим аргументы на блоки. Поскольку аргументы вещественные, мы не будем явно разбивать их, а возьмем максимум в некотором диапазоне вблизи аргумента.
Это дает $$$1,15616$$$, что весьма неплохо. Мы можем еще улучшить ответ, взяв максимум из всех значений $$$f$$$, которые мы когда-либо вычисляли:
Это дает нам $$$1,16278$$$, что очень близко к ожидаемым $$$1,162791$$$. Кажется, что мы нашли хороший метод. Но давайте копнём глубже.
Третья оптимизация
Давайте изменим константу $$$3$$$ в коде. Назовем ее $$$C$$$. Опытным олпрогерам известно, что часто хорошо выбрать $$$C$$$ равной $$$2$$$ (бинарный поиск по производной) или $$$\frac{\sqrt5+1}{2}$$$ (терпоиск с золотым сечением). Поскольку на каждой итерации мы отбрасываем $$$\frac{1}{C}$$$ часть нашего интервала, вероятность того, что максимум окажется внутри отрезанной части, уменьшается с увеличением C.
Выберем $$$C = 100$$$ и запустим тернарный поиск. Как мы уже знаем, взятие максимума из всех вызовов функций — очень хорошая оптимизация, поэтому я сразу ее добавлю.
Если мы запустим его при $$$C = 3$$$, то получим $$$1,13140$$$ (алгоритм тот же, что и в классическом троичном поиске, но мы берем максимум, поэтому ответ намного лучше). Теперь давайте увеличим $$$C$$$ и посмотрим, как увеличится ответ:
Мы запускаем его с $$$C = 30$$$ и получаем $$$1,16275$$$. Запускаем его с $$$C = 100$$$ и получаем... $$$1,15444$$$.
Дело в том, что увеличение $$$C$$$ не гарантирует увеличения ответа.
Четвертая оптимизация
Давайте переберем все значения $$$C$$$ от 3 до 100 и возьмем лучший ответ:
for (int C = 3; C < 100; C++) res = max(res, find_maximum(Weierstrass, C));
Это дает нам $$$1,16279$$$ и работает быстрее, чем разбиение на блоки. Чтобы сравнивать эти подходы дальше, нам нужно изменить функцию, потому что оба метода возвращают значения, которые очень близки к ответу.
Используем $$$a = 0,88$$$ и $$$b = 51$$$ для функции Вейерштрасса. Обратите внимание, что в Desmos невозможно увидеть фактический максимум функции.
Я сравню эти два подхода в Запуске Codeforces.
Я попробовал объединить эти методы вместе, но результат оказался хуже, чем у обоих методов (потому что я использовал $$$1000$$$ итераций вместо $$$10000$$$ и перебор $$$C < 10$$$, чтобы влезть в ТЛ).
Вывод
На рассмотренной мной функции оба подхода достаточно хороши. На реальных соревнованиях я использовал только свой подход (четвертую оптимизацию).
Из недавних задач, 2035E - Монстр, я успешно использовал эту технику. Вот реализация для целочисленных аргументов: 288346163.
Если вы знаете, как найти максимум лучше (не методом имитации отжига), пожалуйста, напишите.