A. Определение лиц

Автор: Monyura

Для решения этой задачи следует перебрать все квадраты 2х2 и проверить, что переставив буквы можно получить слово "face". Это можно удобно сделать, например, отсортировав буквы квадрата в алфавитном порядке и проверив, что отсортированное множество равно "acef"(Отсортированный порядок букв слова "face").

B. Вечеринка в Looksery

Автор: Igor_Kudryashov

При любом раскладе существует такое множество людей, что, если они придут и разошлют сообщения своим контактам, то каждый сотрудник получит количество сообщений отличное от того, что указал Игорь. Покажем как построить это множество. Рассмотрим 2 случая.

Ни одно из чисел, предложенных Игорем, не равно нулю. Тогда если никто не придет на вечеринку, то всем сотрудникам придет по 0 сообщений, и, следовательно, искомое множество — это пустое множество.

Хотя бы одно из чисел Игоря равно нулю. Пусть он предполагает, что i-ому сотруднику достанется 0 сообщений. В этом случае добавим i-ого сотрудника в искомое множество. Он разошлет сообщения всем своим контактам и у него самого количество пришедших сообщений станет равно 1. При добавлении других сотрудников в искомое множество, количество сообщений, пришедших i-ому не уменьшится, а, значит, его можно удалить из рассмотрения. Для людей из списка контактов i-го сотрудника Игорь предсказал некоторые количества сообщений, и т.к. по одному сообщению этим людям уже пришло, из желаемых Игорем чисел нужно вычесть единицу. После этого можно перейти к той же задаче, считая что у нас имеется n - 1 сотрудников. Если оставшееся количество сотрудников равно 0, то искомое множество построено.

C. Игра чётности

Автор: olpetOdessaONU

Если n = k, то ни один ход не может быть совершен. Победитель определяется изначальной суммарной четностью количества жителей. Иначе заметим, что игрок, который делает ход последним, может гарантировать себе победу, если на момент его последнего хода остаются как четные, так и нечетные города — он просто выберет, город с какой четностью сжечь, чтобы получить нужную итоговую четность. Поэтому задача его противника — уничтожить все города какого-то одного типа. Иногда все равно какого, а иногда — нет, это зависит от имени игрока и четности k. Поэтому дальнейшее решение задачи заключается в сравнении количества ходов (n - k) / 2 «непоследнего» игрока с количествами четных и нечетных городов — хватит ли ходов, чтобы их уничтожить. Если последним ходит Станнис, то, в случае четного k, Дейнерис должна сжечь все четные либо все нечетные города. В случае нечетного k, Дейнерис следует сжечь все нечетные города. Если последней ходит Дейнерис, то, в случае четного k ее противник не имеет шансов на победу, а, в случае нечетного k, Станнис должен сжечь все четные города.

D. Признаки Хаара

Автор: Monyura

Эта задача имела сложное условие, но максимально близкое к реальности.

Один из вариантов решения задачи состоит в изучении структуры ответа. Предположим, что у нас есть ответ, т.е последовательность операций: взятие сумм на префикс-прямоугольнике и коэффициентов, на который умножается сумма. Мы можем менять порядок операций, значение признака при этом меняться не будет. Тогда отсортируем операции по правому нижнему углу прямоугольника. Будем применять операции начиная от последний к первой. Решение состоит в том, что бы не применять операции, которые не нужны и применить все те, которые мы обязаны применить. Для этого для каждого пикселя будем поддерживать коэффициент с которым он сейчас входит в значение признака. Изначально этот коэффициент равен 0. Пройдем по каждому пикселю начиная с нижнего правого угла. Если текущий коэффициент не равен  + 1 для пикселя покрытого W и  - 1 для пикселя покрытого B, то пиксель входит в значение признака с неправильным коэффициентом и нам надо его поменять, для этого используем одну операцию. Единственный способ поменять значение этого пикселя теперь, после того как все большие и по ряду и по столбцу просмотрены — это взять сумму на префикс-прямоугольнике с правым нижним углом в этом пикселе. Предположим значение коэффициента должно быть X ( + 1 или  - 1 в зависимости от цвета), а сейчас равно C. Тогда мы должны прибавить сумму на прямоугольнике с коэффициентом X - C к значению признака. Но сделав это, мы так же прибавим X - C к коэффициентам всех пикселей на префикс-прямоугольнике. Это решение может быть реализовано так, как описано за O(n²m²) или за O(nm).

Так же хочется добавить, что от настоящих признаков Хаара данное определение отличается только тем, что настоящие применяются к региону изображения, а не ко всему изображению. Но минимальное число операций можно посчитать по такому же принципу.

E. Саша Круг

Авторы: Krasnokutskiy, 2222

Скоро появится.

F. Юра и разработчики

Автор: Rubanenko

Посмотрим на следующее решение:

Пусть f(l, r) — это решения для подмассива [l, r]. Легко заметить, что f(1, n) — это ответ на поставленную задачу. Как считать f(l, r)? Пусть m — это индекс максимального элемента подмассива [l, r]. Все хорошие подмассивы могут быть разбиты на два непересекающихся множества: те, которые содержат m, и те которые его не содержат. Чтобы посчитать последние можно просто вызвать f(l, m - 1) и f(m + 1, r). Осталось посчитать количество "хороших" подмассивов, которые содержат m, другими словами, количество пар (i, j), что l ≤ i < m < j ≤ r и g(i, m - 1) + g(m + 1, j)%k = 0 (g(s, t) означает a_s + a_s + 1 + ... + a_t). Пусть s — это последовательность частичных сумм массива из условия, то есть s_i = a₁ + a₂ + ... + a_i. Для всех j нам интересно количество i, что s_j - s_i - a_m%k = 0, так что если мы переберем все возможны j, то нам интересно количество таких i, что s_i = s_j - a_m(modk) и l ≤ i < m. Имеем ряд запросов на отрезке вида "сколько есть чисел на отрезке (l, r), что они равны x". Это можно сделать за O(q + k) времени и памяти, где q — количество запросов, которые сгенерировались в ходе рекурсивного вычисления f(1, n). Авторское решение обрабатывает эти запросы в режиме оффлайн, с помощью массива подсчета.

Можно заметить, что в худшем случае мы получим O(n²) запросов, которые очевидно не дадут уложиться в ограничения. Тем не менее, мы можем выбрать, что быстрее: перебрать все возможные j или i. В обоих случаях мы получаем простую сравнимость и запрос на отрезке, описанный выше. Если идти только по меньшему отрезку, то каждый раз, как мы "проходим" по элементу w, он переходит в отрезок, который, как минимум, в два раза меньше, чем тот, которому он принадлежал до этого. Таким образом, каждый элемент окажется в отрезке единичной длины(база рекурсии) за O(log(n)) "проходов" по нему.

Сложность алгоритма O(n × log(n) + k).

G. Счастливая очередь

Авторы: 2222, MrDindows

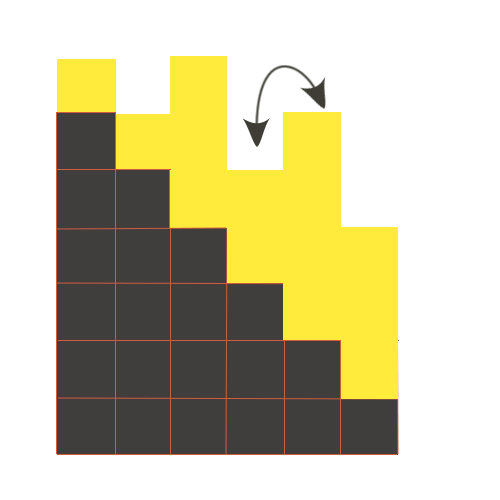
Давайте переформулируем условие в терминах башен определенной высоты, которые будут находиться на лестнице. Тогда количество денег соответствующего человека в очереди будет равно высоте башни вместе с высотой ступеньки, на которой башня стоит. А процесс продвижения в очереди будет эквивалентен подъему одной башни на ступеньку вверх, а та, на чье место она взошла — вниз, как показано на иллюстрации. Тогда, становиться очевидно, что чтобы все башни на ступеньках были отсортированы, достаточно отсортировать башни без учета высот ступенек. Итого сложность сортировки O(nlog(n)).

H. Вырожденная матрица

Автор: Igor_Kudryashov

У вырожденной матрицы строки линейно зависимы, а значит можно представить матрицу B в следующем виде:

Пусть

Положим, что элементы первой строки матрицы A являются координатами точки a₀ на двухмерной плоскости, а элементы второй строки — координатами точки a₁. Представим, что строки матрицы B также являются координатами точек b₀ и b₁. Заметим, что в этом случае прямая, проходящая через точки b₀ и b₁, также проходит через точку (0, 0).

Будем искать ответ на задачу — число d — бинарным поиском. Предположим мы зафиксировали некоторое число d₀ и хотим проверить, существует ли такая матрица B, что

В геометрической интерпретации это означает, что точка b₀ находится в квадрате, с центром в точке a₀ и длиной стороны 2·d₀, а точка b₁, соответственно, в квадрате с такой же длиной стороны и центром в a₁. Таким образом, нам нужно проверить, существует ли прямая, проходящая через точку (0, 0) и пересекающая эти квадраты. Чтобы это сделать, достаточно перебрать вершины одного квадрата, построить прямую, проходящую через выбранную вершину и центр координат и проверить, что она пересекает какую-нибудь из сторон второго квадрата. Затем нужно сделать то же самое, обменяв квадраты. В итоге, если прямая нашлась, то нужно уменьшить границу поиска, иначе расширить.