Hi, In this problem, I am using the idea that AM >= GM just like in the editorial but with slightly different steps.
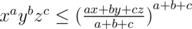
Equality should hold when all elements are equal. So according to me, x = y = z and the solution I arrive at is that x = y = z = S / 3
But this is incorrect as seen from the test case
S = 10
a = 1, b = 6, c = 3
My solution gives x = y = z = 3.33 and hence xa·yb·zc = 169350.87
But the optimal solution is x = 1.0, y = 6.0, z = 3.0 with xa·yb·zc = 1259712
What is the flaw in my math? Is this not a correct way to use GM <= AM? I don't understand why my solution differs from the solution given in the editorial even though the principle behind both is the same.






