628A - Теннисный турнир

The problem suggested by unprost.

Here you can simply model the process. Or you can note that after each match some player drops out. In total n - 1 players will drop out. So the first answer is (n - 1) * (2b + 1). Obviously the second answer is np.

С++ solution 1

С++ solution 2

Complexity: O(log²n), O(logn) or O(1) depends on the realization.

628B - Новый скейтборд

This is one of the problems suyggested by Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.

The key observation is that the number is divisible by 4 if and only if its last two digits forms a number divisible by 4. So to calculate the answer at first we should count the substrings of length one. Now let's consider pairs of consecutive digits. If they forms a two digit number that is divisible by 4 we should increase the answer by the index of the right one.

C++ solution

Complexity: O(n).

628C - Медведь и расстояние между строками

The problem suggested and prepared by Kamil Debowski Errichto.

Complexity: O(n).

628D - Волшебные числа

Kareem Mohamed Kareem_Mohamed suggested the simpler version of the problem.

Denote the answer to the problem f(a, b). Note that f(a, b) = f(0, b) - f(0, a - 1) or what is the same f(a, b) = f(0, b) - f(0, a) + g(a), where g(a) equals to one if a is a magic number, otherwise g(a) equals to zero. Let's solve the problem for the segment [0, n].

Here is described the standard technique for this kind of problems, sometimes it is called 'dynamic programming by digits'. It can be realized in a two ways. The first way is to iterate over the length of the common prefix with number n. Next digit should be less than corresponding digit in n and other digits can be arbitrary. Below is the description of the second approach.

Let z_ijk be the number of magic prefixes of length i with remainder j modulo m. If k = 0 than the prefix should be less than the corresponding prefix in n and if k = 1 than the prefix should be equal to the prefix of n (it can not be greater). Let's do 'forward dynamic programming'. Let's iterate over digit 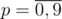in position i. We should check that if the position is even than p should be equal to d, otherwise it cannot be equal to d. Also we should check for k = 1 p should be not greater than corresponding digit in n. Now let's see what will be the next state. Of course i' = i + 1. By Horner scheme j' = (10j + p) mod m. Easy to see that 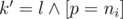. To update the next state we should increase it: z_i'j'k' +  = z_ijk. Of course all calculations should be done modulo 10⁹ + 7.

C++ solution

Complexity: O(nm).