652B - z-sort

The problem was suggested by Smaug.

Easy to see that we can z-sort any array a. Let 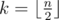be the number of even positions in a. We can assign to those positions k maximal elements and distribute other n - k elements to odd positions. Obviously the resulting array is z-sorted.

const int N = 1010;

int n, a[N];

bool read() {
	if (!(cin >> n)) return false;
	forn(i, n) assert(scanf("%d", &a[i]) == 1);
	return true;
}

int ans[N];

void solve() {
	sort(a, a + n);

	int p = 0, q = n - 1;
	forn(i, n)
		if (i & 1) ans[i] = a[q--];
		else ans[i] = a[p++];
	assert(q + 1 == p);

	forn(i, n) {
		if (i) putchar(' ');
		printf("%d", ans[i]);
	}
	puts("");
}

Complexity: O(nlogn).

652C - Foe Pairs

This is one of the problems suggested by Bayram Berdiyev bayram, Allanur Shiriyev Allanur, Bekmyrat Atayev Bekmyrat.A.

Let's precompute for each value x its position in permutation pos_x. It's easy to do in linear time. Consider some foe pair (a, b) (we may assume pos_a < pos_b). Let's store for each value a the leftmost position pos_b such that (a, b) is a foe pair. Denote that value as z_a. Now let's iterate over the array a from right to left and maintain the position rg of the maximal correct interval with the left end in the current position lf. To maintain the value rg we should simply take the minimum with the value z[lf]: rg = min(rg, z[lf]). And finally we should increment the answer by the value rg - lf + 1.

const int N = 300300;

int n, m;
int p[N];
pt b[N];

bool read() {
	if (!(cin >> n >> m)) return false;
	forn(i, n) {
		assert(scanf("%d", &p[i]) == 1);
		p[i]--;
	}
	forn(i, m) {
		int x, y;
		assert(scanf("%d%d", &x, &y) == 2);
		x--, y--;
		b[i] = pt(x, y);
	}
	return true;
}

int pos[N];
vector<int> z[N];

void solve() {
	forn(i, n) pos[p[i]] = i;
	forn(i, n) z[i].clear();
	forn(i, m) {
		int x = pos[b[i].x], y = pos[b[i].y];
		if (x > y) swap(x, y);
		z[x].pb(y);
	}

	li ans = 0;
	int rg = n;
	nfor(i, n) {
		forn(j, sz(z[i])) rg = min(rg, z[i][j]);
		ans += rg - i;
	}
	cout << ans << endl;
}

Сложность: O(n).

652D - Nested Segments

The problem was suggested by Alexey Dergunov dalex.

This problem is a standard two-dimensional problem that can be solved with one-dimensional data structure. In the same way a lot of other problems can be solved (for example the of finding the maximal weighted chain of points so that both coordinates of each point are greater than the coordinates of the predecessing point). Rewrite the problem formally: for each i we should count the number of indices j so that the following conditions are hold: a_i < a_j and b_j < a_j. Let's sort all segments by the left ends from right to left and maintain some data structure (Fenwick tree will be the best choice) with the right ends of the processed segments. To calculate the answer for the current segment we should simple take the prefix sum for the right end of the current segment.

So the condition a_i < a_j is hold by sorting and iterating over the segments from the right to the left (the first dimension of the problem). The condition b_j < b_j is hold by taking the prefix sum in data structure (the second dimension).

const int N = 1200300;

int n;
pair<pti, int> a[N];

bool read() {
	if (!(cin >> n)) return false;
	forn(i, n) assert(scanf("%d%d", &a[i].x.x, &a[i].x.y) == 2), a[i].y = i;
	return true;
}

int t[N];
vector<int> ys;

inline void inc(int i, int val) {
	for ( ; i < sz(ys); i |= i + 1)
		t[i] += val;
}

inline int sum(int i) {
	int ans = 0;
	for ( ; i >= 0; i = (i & (i + 1)) - 1)
		ans += t[i];
	return ans;
}

int ans[N];

void solve() {
	ys.clear();
	forn(i, n) ys.pb(a[i].x.y);
	sort(all(ys));
	ys.erase(unique(all(ys)), ys.end());
	forn(i, sz(ys)) t[i] = 0;

	sort(a, a + n);
	nfor(i, n) {
		int idx = int(lower_bound(all(ys), a[i].x.y) - ys.begin());
		ans[a[i].y] = sum(idx);
		inc(idx, +1);
	}

	forn(i, n) printf("%dn", ans[i]);
}

Сложность: O(nlogn).