Editorial of Educational Codeforces Round 11

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	166
2	maomao90	163
2	Um_nik	163
4	atcoder_official	161
5	adamant	160
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	nor	153
9	Dominater069	153

660F - Bear and Bowling 4

The problem was prepared by Kamil Debowski Errichto. The problem analysis is also prepared by him.

The key is to use divide and conquer. We need a recursive function f(left, right) that runs f(left, mid) and f(mid+1, right) (where mid = (left + right) / 2) and also considers all intervals going through mid. We will eventually need a convex hull of lines (linear functions) and let's see how to achieve it.

For variables L, R (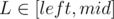 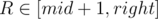$\text{[math]}$ , $\text{[math]}$ ) we will try to write the score of interval [L, R] as a linear function. It would be good to get something close to a_L·x_R + b_L where a_L and b_L depend on L, and x_R depends on R only.

$\text{[math]}$

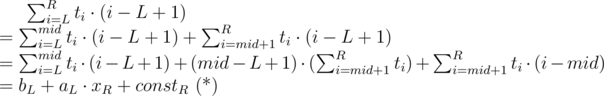
For each L we should find a linear function f_L(x) = a_L·x + b_L where a_L, b_L should fit the equation ( * ):

$\text{[math]}$

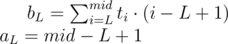
Now we have a set of linear functions representing all possible left endpoints L. For each right endpoint R we should find x_R and const_R to fit equation ( * ) again. With value of x_R we can iterate over functions f_L to find the one maximizing value of b_L + a_L·x_R. And (still for fixed R) we should add const_R to get the maximum possible score of interval ending in R.

Brute Force with functions

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int nax = 1e6 + 5;
ll ans;
ll t[nax];

struct Fun {
	ll a, b;
	ll getValue(ll x) { return a * x + b; }
};

void rec(int first, int last) {
	if(first == last) {
		ans = max(ans, t[first]);
		return;
	}
	int mid = (first + last) / 2;
	
	rec(first, mid); // the left half is [first, mid]
	rec(mid+1, last); // the right half is [mid+1, last]
	
	// we must consider all intervals starting in [first,mid] and ending in [mid+1, last]
	
	vector<Fun> functions;
	ll sum_so_far = 0; // t[i]+t[i+1]+...+t[mid]
	ll score_so_far = 0; // t[i]*1 + t[i+1]*2 + ... + t[mid]*(mid-i+1)
	for(int i = mid; i >= first; --i) {
		sum_so_far += t[i];
		score_so_far += sum_so_far;
		functions.push_back(Fun{mid - i + 1, score_so_far});
	}
	
	sum_so_far = 0;
	score_so_far = 0;
	for(int i = mid+1; i <= last; ++i) {
		sum_so_far += t[i];
		score_so_far += t[i] * (i - mid);
		for(Fun & f : functions) {
			ll score = score_so_far + f.getValue(sum_so_far);
			ans = max(ans, score);
		}
	}
}

int main() {
	int n;
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) scanf("%lld", &t[i]);
	rec(1, n);
	printf("%lldn", ans);
	return 0;
}

Now let's make it faster. After finding a set of linear functions f_L we should build a convex hull of them (note that they're already sorted by slope). To achieve it we need something to compare 3 functions and decide whether one of them is unnecessary because it's always below one of other two functions. Note that in standard convex hull of points you also need something similar (but for 3 points). Below you can find an almost-fast-enough solution with a useful function bool is_middle_needed(f1, f2, f3). You may check that numbers calculated there do fit in long long.

Almost fast enough

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int nax = 1e6 + 5;
ll ans;
ll t[nax];

struct Fun {
	ll a, b;
	ll getValue(ll x) { return a * x + b; }
};

bool is_middle_needed(const Fun & f1, const Fun & f2, const Fun & f3) {
	// we ask if for at least one 'x' there is f2(x) > max(f1(x), f3(x))
	assert(0 < f1.a && f1.a < f2.a && f2.a < f3.a);
	
	// where is the intersection of f1 and f2?
	// f1.a * x + f1.b = f2.a * x + f2.b
	// x * (f2.a - f1.a) = f1.b - f2.b
	// x = (f1.b - f2.b) / (f2.a - f1.a)
	ll p1 = f1.b - f2.b;
	ll q1 = f2.a - f1.a;
	// and the intersection of f1 and f3
	ll p2 = f1.b - f3.b;
	ll q2 = f3.a - f1.a;
	assert(q1 > 0 && q2 > 0);
	// return p1 / q1 < p2 / q2
	return p1 * q2 < q1 * p2;
}

void rec(int first, int last) {
	if(first == last) {
		ans = max(ans, t[first]);
		return;
	}
	int mid = (first + last) / 2;
	
	rec(first, mid); // the left half is [first, mid]
	rec(mid+1, last); // the right half is [mid+1, last]
	
	// we must consider all intervals starting in [first,mid] and ending in [mid+1, last]
	
	vector<Fun> functions;
	ll sum_so_far = 0; // t[i]+t[i+1]+...+t[mid]
	ll score_so_far = 0; // t[i]*1 + t[i+1]*2 + ... + t[mid]*(mid-i+1)
	for(int i = mid; i >= first; --i) {
		sum_so_far += t[i];
		score_so_far += sum_so_far;
		Fun f = Fun{mid - i + 1, score_so_far};
		while(true) {
			int s = functions.size();
			if(s >= 2 && !is_middle_needed(functions[s-2], functions[s-1], f))
				functions.pop_back();
			else
				break;
		}
		functions.push_back(f);
	}
	
	sum_so_far = 0;
	score_so_far = 0;
	for(int i = mid+1; i <= last; ++i) {
		sum_so_far += t[i];
		score_so_far += t[i] * (i - mid);
		for(Fun & f : functions) {
			ll score = score_so_far + f.getValue(sum_so_far);
			ans = max(ans, score);
		}
	}
}

int main() {
	int n;
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) scanf("%lld", &t[i]);
	rec(1, n);
	printf("%lldn", ans);
	return 0;
}

Finally, one last thing is needed to make it faster than O(n²). We should use the fact that we have built a convex hull of functions (lines). For each R you should binary search optimal function. Alternatively, you can sort pairs (x_R, const_R) and then use the two pointers method — check the implementation in my solution below. It gives complexity 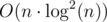$\text{[math]}$ because we sort by x_R inside of a recursive function. I think it's possible to get rid of this by sorting prefixes 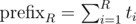$\text{[math]}$ in advance because it's equivalent to sorting by x_R. And we should use the already known order when we run a recursive function for smaller intervals. So, I think $\text{[math]}$ is possible this way — anybody implemented it?

Intended solution with two pointers

// O(n log^2(n))
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int nax = 1e6 + 5;
ll ans;
ll t[nax];

struct Fun {
	ll a, b;
	ll getValue(ll x) { return a * x + b; }
};

bool is_middle_needed(const Fun & f1, const Fun & f2, const Fun & f3) {
	// we ask if for at least one 'x' there is f2(x) > max(f1(x), f3(x))
	assert(0 < f1.a && f1.a < f2.a && f2.a < f3.a);
	
	// where is the intersection of f1 and f2?
	// f1.a * x + f1.b = f2.a * x + f2.b
	// x * (f2.a - f1.a) = f1.b - f2.b
	// x = (f1.b - f2.b) / (f2.a - f1.a)
	ll p1 = f1.b - f2.b;
	ll q1 = f2.a - f1.a;
	// and the intersection of f1 and f3
	ll p2 = f1.b - f3.b;
	ll q2 = f3.a - f1.a;
	assert(q1 > 0 && q2 > 0);
	// return p1 / q1 < p2 / q2
	return p1 * q2 < q1 * p2;
}

void rec(int first, int last) {
	if(first == last) {
		ans = max(ans, t[first]);
		return;
	}
	int mid = (first + last) / 2;
	
	rec(first, mid); // the left half is [first, mid]
	rec(mid+1, last); // the right half is [mid+1, last]
	
	// we must consider all intervals starting in [first,mid] and ending in [mid+1, last]
	
	vector<Fun> functions;
	ll sum_so_far = 0; // t[i]+t[i+1]+...+t[mid]
	ll score_so_far = 0; // t[i]*1 + t[i+1]*2 + ... + t[mid]*(mid-i+1)
	for(int i = mid; i >= first; --i) {
		sum_so_far += t[i];
		score_so_far += sum_so_far;
		Fun f = Fun{mid - i + 1, score_so_far};
		while(true) {
			int s = functions.size();
			if(s >= 2 && !is_middle_needed(functions[s-2], functions[s-1], f))
				functions.pop_back();
			else
				break;
		}
		functions.push_back(f);
	}
	
	vector<pair<ll, ll>> points;
	sum_so_far = 0;
	score_so_far = 0;
	for(int i = mid+1; i <= last; ++i) {
		sum_so_far += t[i];
		score_so_far += t[i] * (i - mid);
		points.push_back({sum_so_far, score_so_far});
		/*for(Fun & f : functions) {
			ll score = score_so_far + f.getValue(sum_so_far);
			ans = max(ans, score);
		}*/
	}
	
	sort(points.begin(), points.end());
	int i = 0; // which function is the best
	for(pair<ll, ll> p : points) {
		sum_so_far = p.first;
		score_so_far = p.second;
		while(i + 1 < (int) functions.size()
			&& functions[i].getValue(sum_so_far) <= functions[i+1].getValue(sum_so_far))
				++i;
		ans = max(ans, score_so_far + functions[i].getValue(sum_so_far));
	}
}

int main() {
	int n;
	scanf("%d", &n);
	for(int i = 1; i <= n; ++i) scanf("%lld", &t[i]);
	rec(1, n);
	printf("%lldn", ans);
	return 0;
}

Complexity: O(nlog²n).

Rev.	By	When	Δ	Comment
en7	Edvard	2016-04-10 18:47:25	66	Tiny change: ' we have $k-1$\nchoic' -> ' we have $m-1$\nchoic'
en6	Edvard	2016-04-09 22:13:28	3481
ru7	Edvard	2016-04-09 21:38:53	202
en5	Edvard	2016-04-09 21:36:44	1097
en4	Edvard	2016-04-09 21:31:11	1280
en3	Edvard	2016-04-09 21:28:04	856
en2	Edvard	2016-04-09 21:17:51	847
ru6	Edvard	2016-04-09 21:09:43	50	Мелкая правка: 'ость: $O(n+k)$.\n\n###' -> 'ость: $O(n)$.\n\n###'
ru5	Edvard	2016-04-09 21:07:54	56
ru4	Edvard	2016-04-09 02:22:21	3780	Мелкая правка: ' log^{2}{n})$.' -
ru3	Edvard	2016-04-09 01:05:26	3539	Мелкая правка: 'mits_{s=1} m^s (m-1)^(n-s) \sum_{k=0' -
en1	Edvard	2016-04-09 00:38:15	9069	Initial revision for English translation
ru2	Edvard	2016-04-09 00:33:39	1030	Мелкая правка: 'cnt_c-1)}2.\n\n 'cnt_c-1)}2$.\n\n
ru1	Edvard	2016-04-09 00:03:25	2956	Первая редакция (опубликовано)

660A - Co-prime Array

660B - Seating On Bus

660F - Bear and Bowling 4

History