678A - Johny Likes Numbers

The problem was suggested by Abdrakhman Ismail bash.

We should find minimal x, so x·k > n. Easy to see that 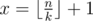. To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.

li n, k;

bool read() {
	return !!(cin >> n >> k);
}

void solve() {
	cout << (n / k + 1) * k << endl;
}

Complexity: O(1).