678A - Johny Likes Numbers
The problem was suggested by Abdrakhman Ismail bash.
We should find minimal x, so x·k > n. Easy to see that 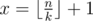 . To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.
. To learn more about floor/ceil functions I reccomend the book of authors Graham, Knuth, Patashnik "Concrete Mathematics". There is a chapter there about that functions and their properties.
Complexity: O(1).
678B - The Same Calendar
The problem was suggested by Arthur Jaworski KingArthur.
Two calendars are same if and only if they have the same number of days and starts with the same day of a week. So we should simply iterate over years and maintain the day of a week of January, 1st (for example). Easy to see that the day of a week increases by one each year except of the leap years, when it increases by two.
Complexity: O(1) — easy to see that we will not iterate more than some small fixed constant times.
678C - Joty and Chocolate
The problem was suggested by Sheikh Monir skmonir.
Easy to see that we can paint with both colours only tiles with the numbers multiple of lcm(a, b). Obviously that tiles should be painted with more expensive colour. So the answer equals to 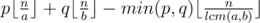 .
.
Complexity: O(log(max(a, b))).
678D - Iterated Linear Function
The problem was suggested by Zi Song Yeoh zscoder.
The problem can be solved using closed formula: it's need to calculate the sum of geometric progression. The formula can be calculated using binary exponentiation.
I'll describe more complicated solution, but it's more general. If we have a set of variables and at each step all variables are recalculating from each other using linear function, we can use binary matrix exponentiation. There is only one variable x in our problem. The new variable x' is calculating using formula A·x + B. Consider the matrix z = [[A, B], [0, 1]] and the vector v = [0, 1]. Let's multiply z and v. Easy to see that we will get the vector v' = [x', 1]. So to make n iterations we should multiply z and v n times. We can do that using binary matrix exponentiation, because matrix multiplication is associative.
As an exercise try to write down the matrix for the Fibonacci numbers and calculate the n-th Fibonacci number in O(logn) time. The matrix and the vector is under the spoiler.
Complexity: O(logn).
678E - Another Sith Tournament
The problem was suggested and prepared by Alexey Dergunov dalex.
Let's solve the problem using dynamic programming. zmask, i — the maximal probability of Ivans victory if the siths from the mask already fought and the i-th sith left alive. To calculate that DP we should iterate over the next sith (he will fight against the i-th sith): 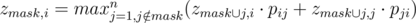 .
.
Time complexity: O(2nn2).
Memory complexity: O(2nn).
678F - Lena and Queries
The problem was suggested by AmirMohammad Dehghan PrinceOfPersia.
Let's interpret the problem geometrically: the pairs from the set are the lines and the problem to find to topmost intersection of the vertical line with the lines from the set.
Let's split the queries to  blocks. Consider the lines added before the current block and that will not deleted in the current block. Let's build the lower envelope by that lines. Now to calculate the answer to the query we should get maximum over the lines from the envelope and the lines from the block before the current query that is not deleted yet. There are no more than
blocks. Consider the lines added before the current block and that will not deleted in the current block. Let's build the lower envelope by that lines. Now to calculate the answer to the query we should get maximum over the lines from the envelope and the lines from the block before the current query that is not deleted yet. There are no more than  lines from the block, so we can iterate over them. Let's find the answers from the envelope for all queries of the third type from the block at once: we should sort them and iterate over envelope using two pointers technique.
lines from the block, so we can iterate over them. Let's find the answers from the envelope for all queries of the third type from the block at once: we should sort them and iterate over envelope using two pointers technique.
Complexity: 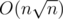 .
.







