Hi, everyone!
I recently implemented 2-3 tree, a balanced tree data structure. The key feature of this tree is, that all the leaves are at the same depth. The implementation is available here: GitHub
Implementation Details
2-3 tree data structure is represented by an enum with three constructors: Tip, Two and Three. Tip is a leaf, with no elements inside. Two is a node with one element and two children, and Three is a node with two elements and three children.
The current implementation supports insert() operation only. It uses a helper function, named insert_sub(). tree.insert_sub(x) inserts an element x to a tree tree, and returns either:
(1) Ok(ret), meaning ret is the resulting tree, or
(2) Err((t1, t2, val)), meaning that the resulting tree has an overcrowded node, so it must be split into two trees t1, t2, with the middle element val moved up.
insert() invokes insert_sub(), and
(1) if the result was Ok(ret), returns ret, or
(2) if the result was Err((t1, t2, val)), returns Two(_, val, t1, t2).
Experiments
Two kinds of experiments were conducted. 1 million elements were inserted into a 2-3 tree, (1) in the ascending order and (2) in a random order. In each iteration, the depth of the 2-3 tree is checked, and if there is a change, the new depth is displayed. The experiment itself took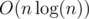 
-time, because the depth of a 2-3 tree can be calculated by checking its leftmost leaf only. (Experiments of treap took O(n2)-time.)
(1) in the ascending order: http://ideone.com/62Seqz
(2) in a random order: http://ideone.com/6DHM21
Here is a graph that illustrates how the depth grows as elements are inserted. The horizontal line shows the number of nodes in the 2-3 tree and the vertical one shows the depth of the 2-3 tree.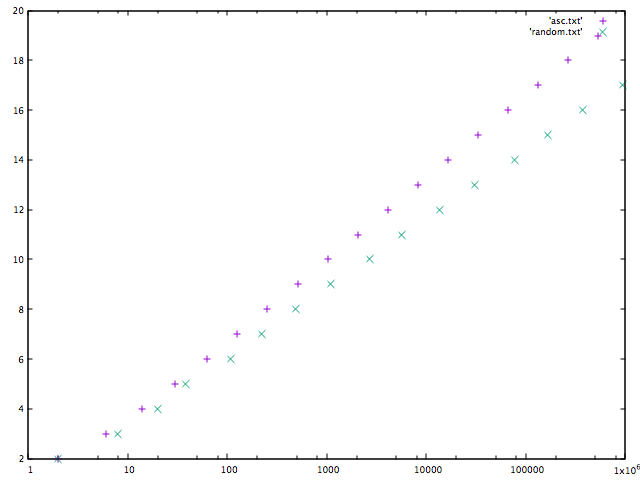 
Note that one has not only an asymptotic upper bound 
of the depth, but also a strict upper bound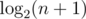 
. That is because all the leaves of the 2-3 tree are at the same depth. (A 2-3 tree of depth d has at least 2d - 1 nodes.) It is also worth noting that unlike treap, there is no decrease of depth in the random case.
Conclusion
We have the 2-3 tree data structure, implemented on Rust!
References
The code is available here: https://github.com/koba-e964/contest/blob/61af81645a9c1287e3302642696f4fb5e5db47fb/comm/TwoThreeTree.rs
http://ideone.com/62Seqz
http://ideone.com/6DHM21
The implementation was done with the aid of this slide: https://www.slideshare.net/sandpoonia/23-tree
