A simple introduction to "Segment tree beats"

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Hi, I’d like to introduce a simple trick about segment tree in this blog as I promised in this comment. Sorry for the long delay, as a sophomore in Peking University, I've just finished a tired semester and a painful final exam. And now I finally have enough time to do a simple introduction to this interesting algorithm.

It may be a huge project for me since my English is not good. I think I will finish this blog in several steps and I will try to finish it as soon as possible :)

In China, all of the 15 candidates for the Chinese National Team are asked to write a simple research report about algorithms in informatics Olympiad, and the score will be counted in the final selection. There are many interesting ideas and algorithms in these reports. And I find that some of them are quite new for competitors in CF although they are well known in China for the final standings of some recent contests. For example, In the last contest CF Round #458, the problem G can be easily solved using set power series (I don’t know how to describe it in English so I just use the phrase given by Baidu translate) in O(2ⁿⁿ²) which is import in China by vfleaking in 2015.

This blog is about my report which is written about two years ago. I am satisfied with this work although there is a flaw about time complexity. xyz111 gave me a lot of inspiration, and the name “Segment tree beats” is given by C_SUNSHINE which is from a famous Japanese anime “Angel Beats”.

Here is the link about the Chinese version of this report.

Part1. What it can do.

This work have two part:

Transform interval max/min (for 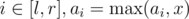$\text{[math]}$ ) operations into interval add/minus operations in O(1) or $\text{[math]}$
Transform history max/min/sum queries into interval max/min operations in O(1).

Here are some sample problems I used in my report. At first you have a array A of length n and two auxiliary arrays B, C. Initially, B is equal to A and C is all zero.

Task 1. There are two kinds of operations:

For all $\text{[math]}$ , change A_i to max(A_i, x)
Query for the sum of A_i in [l, r]

It can be solved in $\text{[math]}$

Task 2. We can add more operations to Task 1:

For all $\text{[math]}$ , change A_i to max(A_i, x)
For all $\text{[math]}$ , change A_i to min(A_i, x)
For all $\text{[math]}$ , change A_i to A_i + x, x can be a negative number
Query for the sum of A_i in [l, r]

It can be solved in $\text{[math]}$ and I could not proved the exact time complexity yet, maybe It is still $\text{[math]}$ ;)

Task 3. And we can query for some other things:

For all $\text{[math]}$ , change A_i to max(A_i, x)
For all $\text{[math]}$ , change A_i to min(A_i, x)
For all $\text{[math]}$ , change A_i to A_i + x, x can be a negative number
Query for the sum of B_i in [l, r]

After each operation, for each i, if A_i changed in this operation, add 1 to B_i.

It’s time complexity is the same as Task 2.

Task 4. We can also deal with several arrays synchronously. Assume there are two arrays A₁ and A₂ of length n.

For all $\text{[math]}$ , change A_a, i to min(A_a, i, x)
For all $\text{[math]}$ , change A_a, i to A_a, i + x, x can be a negative number
Query for the max A_1, i + A_2, i in [l, r]

It can be solved in $\text{[math]}$ and if there are k arrays, the time complexity will be raised to 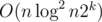$\text{[math]}$ .

Task 5. And there are some tasks about history informations.

For all $\text{[math]}$ , change A_a, i to A_a, i + x, x can be a negative number.
Query for the sum of B_i in [l, r].
Query for the sum of C_i in [l, r]

After each operation, for each i, change B_i to max(B_i, A_i) and add A_i to C_i.

The query for B_i can be solved in $\text{[math]}$ and the query for C_i can be solved in $\text{[math]}$ .

Task 6. We can even merged the to parts together.

For all $\text{[math]}$ , change A_a, i to max(A_a, i, x)
For all $\text{[math]}$ , change A_a, i to A_a, i + x, x can be a negative number.
Query for the sum of B_i in [l, r].

After each operation, for each i, change B_i to min(B_i, A_i).

It can be solved in 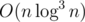$\text{[math]}$ .

There are 11 sample tasks in my report and here are 6 of them. All of them are interesting and are hard to solve using the traditional techniques such as lazy tags.

In the next update, I suppose to introduce the main idea of this trick without the prove of the time complexity. Since I’m traveling in Harbin and the temperature of thirty degrees below zero makes me really tired, I want to go to rest early. Sorry for the interruption and I’ll try to finish the rest part as soon as possible :)

Rev.	By	When	Δ	Comment
en21	jiry_2	2018-01-28 04:43:36	12	Tiny change: 'ven by [usr:xyz111] ' -> 'ven by [user:xyz111] '
en20	jiry_2	2018-01-27 14:17:29	117
en19	jiry_2	2018-01-27 14:08:14	1735	Tiny change: '90605.png)\n\nThus, ' -> '90605.png){:height="100px" width="400px"}\n\nThus, '
en18	jiry_2	2018-01-27 13:40:43	7	Tiny change: ', we will also use the t' -> ', we will still use the t'
en17	jiry_2	2018-01-27 13:39:20	1607	Tiny change: 'the total number of $\Phi(' -> 'the total increase of $\Phi('
en16	jiry_2	2018-01-27 12:56:03	365
en15	jiry_2	2018-01-27 12:43:04	4659	Add the proof for task 1
en14	jiry_2	2018-01-27 12:35:19	33
en13	jiry_2	2018-01-27 11:56:33	5	Tiny change: '& r <= rr and max_value' -> '& r <= rr && max_value'
en12	jiry_2	2018-01-27 10:29:51	49
en11	jiry_2	2018-01-27 10:12:20	4	Tiny change: 'Historic maximal value' -> 'Historic minimal value'
en10	jiry_2	2018-01-26 17:01:38	2806
en9	jiry_2	2018-01-25 17:21:34	136
en8	jiry_2	2018-01-25 17:17:52	5446	Tiny change: 'affected. \n2. When ' -> 'affected. So we can return immediately.\n2. When '
en7	jiry_2	2018-01-25 13:07:08	12
en6	jiry_2	2018-01-24 18:05:58	1	Tiny change: 'rged the to parts to' -> 'rged the two parts to'
en5	jiry_2	2018-01-24 18:02:56	3	Tiny change: 'in China for the final' -> 'in China from the final'
en4	jiry_2	2018-01-24 17:40:31	5	Tiny change: '2)$ which is import in China ' -> '2)$ which was imported in China '
en3	jiry_2	2018-01-24 17:26:29	2	Tiny change: ') in $O(2^n n^2)$ whi' -> ') in $O(2^{n} n^2)$ whi'
en2	jiry_2	2018-01-24 17:25:28	1	Tiny change: ' in $O(2^nn^2)$ whic' -> ' in $O(2^n n^2)$ whic'
en1	jiry_2	2018-01-24 17:24:51	5058	Initial revision (published)

Part1. What it can do.

History