Problem Statement
We are going to deal with the well known knapsack problem with an additional constraint. We are given a list of N items and a knapsack of size W. Every item has a cost ci associated with it (1 ≤ i ≤ N). We can select some items from the list such sum of the cost of all the selected items does not exceed W. The goal is tell for all w (0 ≤ w ≤ W), if we can select any number of items such that their total cost equals w. This is also known as the 0/1 knapsack problem. This can be easily solved in O(NW) time complexity using standard knapsack approach.
The addition constraint we have is 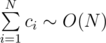 .
.
The bounded knapsack problem
The bounded knapsack problem is like the 0/1 knapsack problem, except in this we are also given a count for each item. In other words, each item has a count si associated with it and we can select an item si times (1 ≤ i ≤ N).
Solving bounded knapsack problem
The solution is simple. Let dp[i][j] be the minimum count of ith item that has to be used to get a total cost of j while using some number (possibly 0) of first i items. If a total cost of j can not be obtained using first i items, then dp[i][j] = - 1. The following code is used to calculate the dp[i][j],
if(dp[i-1][j] >= 0)
dp[i][j] = 0;
else if(dp[i][j - c[i]] >= 0 and dp[i][j - c[i]] < s[i])
dp[i][j] = dp[i][j - c[i]] + 1;
else
dp[i][j] = -1;
Here, c[i] is the cost and s[i] is the count for ith item. Also, dp[0][j] = - 1 for all 1 ≤ j ≤ W and dp[0][0] = 0. Time complexity is O(NW).
Optimizing 0/1 Knapsack
Now we can present a faster solution to our problem. Notice that number of items is N and 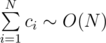 . Hence, there can only be
. Hence, there can only be 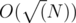 unique costs. So we convert our problem to a bounded knapsack problem with
unique costs. So we convert our problem to a bounded knapsack problem with 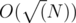 unique items having some count. This can be solved in
unique items having some count. This can be solved in 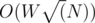 !!!
!!!
PS: I wrote this blog since I could not find a good source on the internet to learn about this approach. I hope there is no error since I really didn't read about this anywhere and worked out this approach myself.






