Hello!

Bubble Cup 2018 Round 2 just finished, so I decided to ask about a correct solution problem NEO. I guess a lot of people passed it in 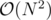with the C++ pragma optimizations or with some greedy optimizations. My team also passed it like that.

In this blog I'll share my idea. If someone has solved it in a similar way I will really appreciate if he shares his code because honestly the idea is really annoying to implement. If anyone has another solution, which is better than 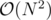I will really love to know the idea.

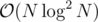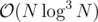So the solution I had in mind is or depending how we implement our query. First we will have the standard DP: dp_i = max_j < i(dp_j + sum_i * i + sum_j * j - j * sum_i - i * sum_j) which can be reformed to dp_i = sum_i * i + max_j < i((dp_j + sum_j * j) + ( - j * sum_i) + ( - i * sum_j)). Well we can still reform this equation the the following: .

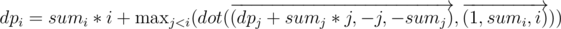Now basically we only need to implement a data structure for the following operations:

1. Add a vector to our DS.

2. Given a vector, find the one with the largest dot product, when multiplied with it.

I found a paper which claimed that the following operations can be implemented with a 3D convex hull and another one which claimed that these operations can be converted to dynamic furthest point search, but unfortunately I cannot find the latter again (this happens when you do not bookmark anything). Also both presented data structures/algorithms were really annoying to implement.

So has anyone solved this problem in a legit way and if yes, can he share his solution. Thanks in advance :)