Здравствуйте! На acmp.ru есть интересная задача — самая сложная задача с полуфинала ВКОШП 2016/2017 Красноярского края. Ниже приведу краткое условие.
Есть циклический массив длины n (1 ≤ n ≤ 105) из целых неотрицательных чисел (все его элементы расположены по кругу), сумма элементов которого не превосходит 109. Требуется для каждого k от 1 до n определить, можно ли разбить отрезок [1..n] массива на k непересекающихся отрезков, сумма элементов в которых равна и каждый элемент покрыт хотя бы одним отрезком. Так как массив циклический, то за элементом с индексом n следует элемент с индексом 1, таким образом, последний отрезок может переходить через границу массива.
Раньше этот пост содержал просьбу помочь, так как не проходило мое решение. После обсуждения и изучения контр-тестов, предоставленных YANORMALNOSUPERGOOD, выяснилось, что это решение и не должно проходить, так как оно основывается на жадности, после чего было придумано следующее решение: для каждого делителя si суммы всех элементов S для каждого отрезка [l, r], содержащего начальный элемент массива, при помощи бинарного поиска и префикс-сумм предпринимается попытка построить еще ki = 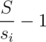 отрезков (ki ≤ n), сумма на которых в точности равна si. Если я ничего не перепутал, то это решение занимает O(count(ki)·n + sum(ki)·log(n)) ≈ O(n4 / 3·log(n)·log(log(n))) по времени. На сервере оно работает за 1.5 секунды.
отрезков (ki ≤ n), сумма на которых в точности равна si. Если я ничего не перепутал, то это решение занимает O(count(ki)·n + sum(ki)·log(n)) ≈ O(n4 / 3·log(n)·log(log(n))) по времени. На сервере оно работает за 1.5 секунды.
Вопрос: можно ли решить оптимальнее, легче (возможно, за один проход по массиву), и нет ли контр-тестов, которые должны вызывать TLE у решения выше?
UPD: Aeon и YANORMALNOSUPERGOOD показали, что оптимальнее решить можно, а именно, за время O(n·numberOfDivisors(S). Причем, в оценке участвуют только делители, которые не превосходят n. Ключевой момент — избавиться от бинарного поиска, который выполнялся sumOfDivisors(S) раз. Для этого можно перейти к динамическому программированию и для одного делителя предподсчитать определенную величину, которая позволит за O(1) отвечать на запрос о максимальном количестве искомых отрезков. Решения с указанной асимптотикой приведены в комментариях здесь и здесь.
Возможно, асимптотику можно еще улучшить, воспользовавшись тем фактом, что если мы выяснили, что для какого-то делителя суммы ответ 0, то и для всех делителей, кратных ему, ответ 0, а если для какого-то делителя ответ 1, то и для всех делителей, на которые он делится, ответ 1.






