Summary: This blog talks about solving two kinds of simple recursions: F(n + 1) = aF(n) + b and F(n + 1) = aF(n) + bF(n - 1)

1. Preliminary Knowledge

(1) The solution of recursion F(n + 1) = aF(n) is F(n) = a^n - 1F(1).

(2) The solution of recursion F(n + 1) = F(n) + a is F(n) = (n - 1)a + F(1).

(3) The recursion F(n + 1) = kF(n) is the same as F(n) = kF(n - 1), also F(n + 1) = aF(n) + bF(n - 1) is the same as F(n) = aF(n - 1) + bF(n - 2) in this blog.

2. Solving F(n + 1) = aF(n) + b, a, b are constants, a > 1

The main idea is to create another function G(n) that satisfy G(n) = kG(n - 1) with constant k, solve G(n), and then solve F(n).

F(n + 1) = aF(n) + b

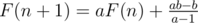
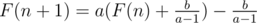
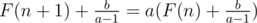
Let 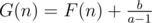we have

G(n) = aG(n - 1)

G(n) = a^n - 1G(1)

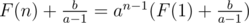
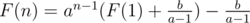
3. Solving F(n + 1) = aF(n) + bF(n - 1), a, b are constants

The main idea is also to create G(n), but the method is different, and the function G(n) is more complicated.

F(n + 1) = aF(n) + bF(n - 1)

Let α, β be two real numbers that satisfy α + β = a, αβ =  - b, α ≤ β we have

F(n + 1) = (α + β)F(n) - αβF(n - 1)

F(n + 1) - αF(n) = βF(n) - αβF(n - 1)

F(n + 1) - αF(n) = β(F(n) - αF(n - 1))

Let G(n) = F(n + 1) - αF(n), also we have G(n - 1) = F(n) - αF(n - 1)

G(n) = βG(n - 1), therefore G(n + 1) = βG(n)

G(n) = β^n - 1G(1)

F(n + 1) - αF(n) = β^n - 1(F(2) - αF(1)) (1)

Similarly, because of F(n + 1) = (α + β)F(n) - αβF(n - 1) we have

F(n + 1) - βF(n) = αF(n) - αβF(n - 1)

F(n + 1) - βF(n) = α(F(n) - βF(n - 1))

Let H(n) = F(n + 1) - βF(n) we have H(n - 1) = F(n) - βF(n - 1)

H(n) = αH(n - 1), therefore H(n + 1) = αH(n)

H(n) = α^n - 1H(1)

F(n + 1) - βF(n) = α^n - 1(F(2) - βF(1)) (2)

Suppose that α ≠ β

(2) - (1) we have

(α - β)F(n) = α^n - 1(F(2) - βF(1)) - β^n - 1(F(2) - αF(1))

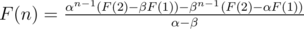
How to get the proper α, β?

According to the Vieta Theorem, α, β is the two solutions of quadratic equation x² - ax - b = 0.

Of course, we only talk about α ≠ β, a² ≠  - 4b.

Just solving the quadratic equation is OK. (You can get the formula for solving a quadratic equation from the problem 530A - Quadratic equation.)

This equation is called the characteristic equation.

Example: Solve the Fibonacci sequence F(1) = 1, F(2) = 1, F(n) = F(n - 1) + F(n - 2).

Solution: Here we have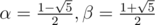

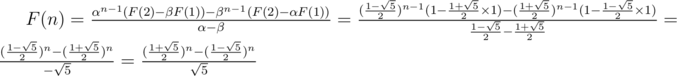
(because we have )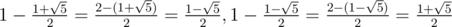

What will happen if α = β, a² = 4b?

I am sorry that I cannot solve it yet.

I'll try to solve it later.