The first step is how to deal with (f(x))k.Here we can use Stirling Number of the second kind. Let's define S(i, j) the number of ways to put i different elements into j sets and there are no empty set.Note that the all j sets are the same.For example S(3, 2) = 3.The three ways are {{1}, {2, 3}}, {{1, 2}, {3}}, {{1, 3}, {2}}.So we have:
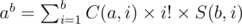
How to proof it?ab is the number of ways to put b different elements into a different sets and empty sets are allowed.The other side of the equation means we select i sets from a sets and arrange them in i! different orders and put b different elements in it. So the fomula in the statement becomes:
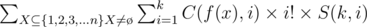
Which equals to:
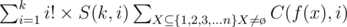
For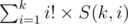 
we can use the following O(k2) DP to calculate all S(k, i).
Which means we consider the ith element.It can form a set by its own.Or you can insert is into one of those j sets.
For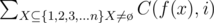 
we use tree DP. Let's define gij the number of sets X plus the number of some tricky situation when we select j edges in the subtree of node i.In addition,there should exist a node 
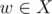for every selected edge (u, v)(depthu < depthv) that w is in the subtree of v.The initial value is:
Means we can choose node i or not. When we add an child ch of i into our DP states we go through every possible l and we select l edges in the subtree of ch or we select l - 1 edges in the subtree of ch and select edge (i, ch).So we have:
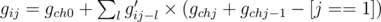
Where g' is the previous state without add informations of ch.Note that in order to hold "there should exist a node 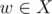for every selected edge (u, v)(depthu < depthv) that w is in the subtree of v" we have to minus 1 invalid state which is "select edge (u, v) but select no node in the subtree of ch". And for answer,we have to know what are those some tricky situation.For example,we only select nodes from one subtree of i and some of the edges cannot be selected according to the defination of f because none of their ancestors is selected.So we have to go through all the children of i and minus them.Let's define hij be the number of sets X when we select j edges in the subtree of node i.So we have:
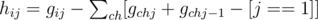
And now we finally have:
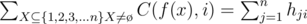
The total complexity is O(nk + k2). My code:https://mirror.codeforces.com/contest/1097/submission/48058882
