Hello, Codeforces! The reason why I am writing this blog is that my ACM/ICPC teammate calabash_boy is learning this technique recently(he is a master in string algorithms,btw), and he wanted me to provide some useful resources on this topic. I found that although many claim that they do know this topic well, problems concerning inclusion-exclusion principle are sometimes quite tricky and not that easy to deal with. Also, after some few investigations, the so-called "Inclusion-Exclusion principle" some people claim that they know wasn't the generalized one, and has little use when solving problems. So, what I am going to pose here, is somewhat the "Generalized Inclusion-Exclusion Principle". Most of the describing text are from the graduate text book Graduate Text in Mathematics 238, A Course in Enumeration, and the problems are those that I encountered in real problem set, so if possible, I'll add a link to the real problem so that you can solve it by yourself. I'll start with the basic formula, one can choose to skip some of the text depending on your grasp with the topic.
Consider a finite set X and three subsets A, B, C, To obtain 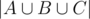 , we take the sum
, we take the sum 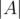 +
+ 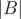 +
+ 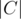 . Unless A, B, C are pairwise distinct, we have an overcount, since the elements of
. Unless A, B, C are pairwise distinct, we have an overcount, since the elements of  has been counted twice. So we subtract
has been counted twice. So we subtract  . Now the count is correct except for the elements in
. Now the count is correct except for the elements in 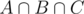 which have been added three times, but also subtracted three times. The answer is therefore
which have been added three times, but also subtracted three times. The answer is therefore
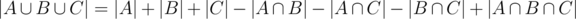
, or equivalently,
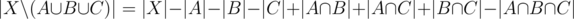
The following formula addresses the case applied to more sets.
The Restricted Inclusion-Exclusion Principle Let A1, A2, ..., An be subsets of X. Then
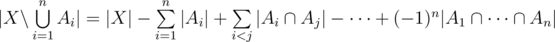
This is a formula which looks familiar to many people, I'll call it The Restricted Inclusion-Exclusion Principle, it can convert the problem of calculating the size of the union of some sets into calculating the size of the intersection of some sets. It's not hard to prove the correctness of this formula, we can just check how often an element 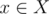 is counted in both sides. If
is counted in both sides. If 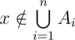 , then it's counted once on either side. Suppose
, then it's counted once on either side. Suppose 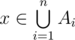 , and more precisely, that x is in exactly m of the sets Ai. The count on the left-hand side is 0, and on the right hand side, we have
, and more precisely, that x is in exactly m of the sets Ai. The count on the left-hand side is 0, and on the right hand side, we have
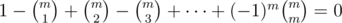
for m ≥ 1, thus the equality holds.
Let's see an example problem Co-prime where this principle could be applied: Given N, L, R, you need to compute the number of integers x in the interval [L, R] such that x is coprime with N, that is, gcd(x, N) = 1. Constraints: 1 ≤ N ≤ 109, 1 ≤ L ≤ R ≤ 1015.
The standard interpretation leads to the principle of inclusion-exclusion. Suppose we are given a set X, called the universe, and a set E = {e1, e2, ..., en} of properties that the elements of X may or may not process. Here we can define the properties as we like, such as e = " ≤ 5", 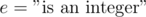 , or even
, or even 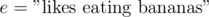 . Let Ai be the subset of elements that enjoy property ei(and possibly others). Then
. Let Ai be the subset of elements that enjoy property ei(and possibly others). Then 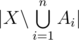 is the number of elements that process none of the properties. Clearly, Ai1, Ai2, ..., Ait is the set of elements that possess the properties ei1, ei2, ..., eit(and maybe others). Using the notation
is the number of elements that process none of the properties. Clearly, Ai1, Ai2, ..., Ait is the set of elements that possess the properties ei1, ei2, ..., eit(and maybe others). Using the notation
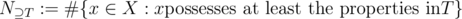
,



 and then find all prime factors
and then find all prime factors 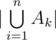 , which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is
, which may be hard to compute directly. However, using the restricted inclusion-exclusion principle, we can convert the problem into computing the size of the intersection of sets, which is trivial. Time complexity is 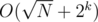 , with
, with 

