I decided to write this blog, as a lot of people were requesting for the editorial of Shortest Path Constrained problem from CodeNation Hiring Test, held on 26th January, 2019
Problem
Statement
There is a weighted undirected graph with N nodes and M edges. You are also given X different sets of nodes — S1 to Sx. You have to give the shortest possible distance between a start node — a and a destination node — b, along a path following the following rule: For all i < j, before visiting a node in Sj, you must visit all the nodes in Si.
The distance is defined as sum of weights of edges along the path traversed.
Note :-
- The path must contain all the nodes in union of Si for all 1 ≤ i ≤ X
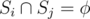 for all 1 ≤ i, j ≤ X and i ≠ j.
for all 1 ≤ i, j ≤ X and i ≠ j.- The path may go through any node, including a and b, more than once. The constraint is that it must end at b
Constraints
- 2 ≤ N ≤ 100
- 0 ≤ w ≤ 100000
- 0 ≤ X ≤ 10
- 1 ≤ |Si| ≤ 10 for all i ≤ X
- Nodes are numbered from 0 to N - 1
- The graph does not contains multiple edges or self edges, and is connected
Solution
Let us first solve the problem of how to visit all the nodes in a set Si, in shortest possible distance, such that we end up at node x. This problem can be solved using dp + bitmask. Suppose dp[bitmask][x] stores the minimum distance, for this particular set, such that the nodes with bits set to 1 in bitmask are visited, and we end up at node x. Now for all k such that kth bit is 0 in bitmask, we can update dp[bitmask|k][k] = min(dp[bitmask][x] + dist(x, k), dp[bitmask|k][k])






