#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

I decided to write this blog, as a lot of people were requesting for the editorial of Shortest Path Constrained problem from CodeNation Hiring Test, held on 26th January, 2019

Problem

Statement

There is a weighted undirected graph with N nodes and M edges. You are also given X different sets of nodes — S₁ to S_x. You have to give the shortest possible distance between a start node — a and a destination node — b, along a path following the following rule: For all i < j, before visiting a node in S_j, you must visit all the nodes in S_i.

The distance is defined as sum of weights of edges along the path traversed.

Note :-

The path must contain all the nodes in union of S_i for all 1 ≤ i ≤ X
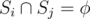$\text{[math]}$ for all 1 ≤ i, j ≤ X and i ≠ j.
The path may go through any node, including a and b, more than once. The constraint is that it must end at b

Constraints

2 ≤ N ≤ 100
0 ≤ w ≤ 100000
0 ≤ X ≤ 10
1 ≤ |Si| ≤ 10 for all i ≤ X
Nodes are numbered from 0 to N - 1
The graph does not contains multiple edges or self edges, and is connected

Solution

Let us first solve the problem of how to visit all the nodes in a set S_i, in shortest possible distance, such that we end up at node x. This problem can be solved using dp + bitmask. Suppose dp[bitmask][x] stores the minimum distance, for this particular set, such that the nodes with bits set to 1 in bitmask are visited, and we end up at node x. Now for all k such that k^th bit is 0 in bitmask, we can update dp[bitmask|k][k] = min(dp[bitmask][x] + dist(x, k), dp[bitmask|k][k]).

Unable to parse markup [type=CF_TEX]

to k and can be precalculated using Floyd-Warshall Algorithm.

Now, in this problem, we need to do the above for all the sets, while making sure the nodes from next sets are not visited. To do that, we maintain a list of illegal nodes. When we visit a set S_i, we remove the nodes of this set from the illegal list. Now, we create an auxiliary adjacency matrix, which does not contain the nodes from the illegal list. Now we can run the above dp.

We can initialize the dp for S_i + 1 using the dp for S_i

Code

Click to Expand

#include <bits/stdc++.h>

using namespace std;

int n, m, x, source, sink;

int adj[100][100];
int currAdj[100][100];
set<int> notAllowed;
vector<vector<int> > sets;

void initialize() {
	memset(adj, -1, sizeof(adj));
	memset(currAdj, -1, sizeof(currAdj));
	for(int i=0 ; i<100 ; ++i) {
		adj[i][i] = 0;
	}
	scanf("%d %d", &n, &m);
	for(int i=0 ; i<m ; ++i) {
		int u, v, w;
		scanf("%d %d %d", &u, &v, &w);
		adj[u][v] = w;
		adj[v][u] = w;
	}

	scanf("%d", &x);
	sets.resize(x);
	for(int i=0 ; i<x ; ++i) {
		int sx, temp;
		scanf("%d", &sx);
		for(int j=0 ; j<sx ; ++j) {
			scanf("%d", &temp);
			sets[i].push_back(temp);
			notAllowed.insert(temp);
		}
	}
	scanf("%d %d", &source, &sink);
}

void updateCurrAdjFromNotAllowed() {
	for(int i=0 ; i<n ; ++i) {
		currAdj[i][i] = 0;
		for(int j=i+1 ; j<n ; ++j) {
			if(notAllowed.find(i)!=notAllowed.end() || notAllowed.find(j)!=notAllowed.end())
				continue;
			currAdj[i][j] = adj[i][j];
			currAdj[j][i] = adj[j][i];
		}
	}
}

void runFloydWarshall() {
	for(int k=0 ; k<n ; ++k) {
		for(int i=0 ; i<n ; ++i) {
			for(int j=0 ; j<n ; ++j) {
				if(currAdj[i][k] == -1 || currAdj[k][j] == -1)
					continue;
				currAdj[i][j] = min((currAdj[i][j]==-1?INT_MAX:currAdj[i][j]), currAdj[i][k] + currAdj[k][j]);
			}
		}
	}
}

void completeDp(vector<vector<int> > &dp, int setSize, int setIndex) {
	int bmLimit = (1<<setSize); 
	for(int bm=0 ; bm<bmLimit ; ++bm) {
		for(int j=0 ; j<setSize ; ++j) {
			if(dp[bm][j] == -1)
				continue;
			for(int k=0 ; k<setSize ; ++k) {
				if(((bm>>k)&1) == 1)
					continue;
				int newBm = bm | (1<<k);
				if(currAdj[sets[setIndex][j]][sets[setIndex][k]] != -1)
					dp[newBm][k] = min((dp[newBm][k]==-1?INT_MAX:dp[newBm][k]), dp[bm][j] + currAdj[sets[setIndex][j]][sets[setIndex][k]]);
			}
		}
	}
}

int main() {
	initialize();
	vector<int> distanceToEndAt(n, -1);
	distanceToEndAt[source] = 0;
	queue<int> q;
	q.push(source);
	for(int i=0 ; i<sets.size() ; ++i) {
		for(int j=0 ; j<sets[i].size() ; ++j)
			notAllowed.erase(sets[i][j]);
		updateCurrAdjFromNotAllowed();
		runFloydWarshall();
		vector<vector<int> > dp(1<<(sets[i].size()), vector<int>(sets[i].size(), -1));
		while(!q.empty()) {
			int fr = q.front();
			q.pop();
			for(int j=0 ; j<sets[i].size() ; ++j) {
				if(currAdj[fr][sets[i][j]] != -1) {
					dp[1<<j][j] = min((dp[1<<j][j]==-1?INT_MAX:dp[1<<j][j]), distanceToEndAt[fr] + currAdj[fr][sets[i][j]]);
				}
			}
		}
		completeDp(dp, sets[i].size(), i);
		int finalBm = (1<<sets[i].size())-1;
		for(int j=0 ; j<sets[i].size() ; ++j) {
			if(dp[finalBm][j] != -1) {
				distanceToEndAt[sets[i][j]] = dp[finalBm][j];
				q.push(sets[i][j]);
			}
		}
	}
	int ans = -1;
	while(!q.empty()) {
		int fr = q.front();
		q.pop();
		if(ans==-1 || (currAdj[fr][sink]!=-1 && ans>currAdj[fr][sink]+distanceToEndAt[fr]))
			ans = currAdj[fr][sink] + distanceToEndAt[fr];
	}
	printf("%d", ans);
}

Sample Cases (Including corner cases)