You are given a rectangular board of A rows where each row contains B square shaped boxes.
Each square box has a unique integer written on it in the row major order (starting from 1 to A* B). The top left square box has value 1 and bottom right square box has value A*B.
You are asked to cut the board into exactly C parts such that each square box is present in exactly one part.
Note: It is not necessary that each cut starts from the boundary of the board.
Some possible ways are:
- A = 3, B = 3, C = 2
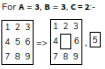
- A = 2, B = 2, C = 2:
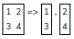
Find the number of different ways in which you can have C parts of the rectangular board. Two ways are considered different if there is at least one part obtained in one way whose identical part is not present in the other way.
1 <= A <= 15
1 <= B <= 15
1 <= A*B <= 15
1 <= C <= A*B
Sample Input: A = 2, B = 2, C = 2
Sample Output: 6
I was asked this question in a coding round. The recurrence might be related to Stirling numbers of the second kind. Any ideas?






