- Contest Link: Programming Contest #1 (Chapter 'Ramayan')
- Problem Setter: Pallove
Logic (Explanation)
Problem Setter's Code
-/-/-
- Problem Setter: Pallove
Logic (Explanation)
Problem Setter's Code
-/-/-
- Problem Setter: Pallove
Logic (Explanation)
Problem Setter's Code
-/-/-
- Problem Setter: Pallove
Logic (Explanation)
Let’s create the two-dimensional array dis[node][deg], which stores the ancestor of node at distance 2deg.
If we fill this dis array, we can answer every query in lg(n) time, using Binary Lifting.
dis[node][0] = parent(node), for every node (except root)
dis[root][0] = -1, for root node.
So, now for deg from 1 to lg(n) and for each node,
dis[node][deg] = dis[dis[node][deg-1]][deg-1].
So, now, for each query node d, convert d into its binary representation and for every set bit in this binary representation, we replace node to dis[node][set-bit position from right], till the value of node doesn't become -1 or till all the set-bits of d are iterated.
Time Complexity: `O((n+q)*



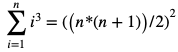
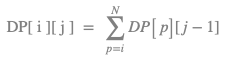 where
where 


