Warning: The following contains graphic depictions of geometry, precision errors, and degenerate cases. Viewer discretion is advised.
Prerequisites
I assume the reader is familiar with:
- 2D Convex Hulls
- 3D Vector Operations (dot and cross products)
Introduction
Recall that in the 2D convex hull problem, you are given a set of 2D points, and you must compute the smallest convex polygon containing all the given points. By convex, we mean that for any two points $$$A$$$ and $$$B$$$ inside the polygon, the entire line segment $$$AB$$$ is also inside the polygon.
The problem in 3D is completely analogous. You are given $$$n$$$ 3D points, and you must compute the smallest convex polyhedron containing all the given points. Similarly, a polyhedron is convex if for any two points $$$A$$$ and $$$B$$$ inside the polyhedron, the line segment $$$AB$$$ is also inside the polyhedron.
In the 2D case, it is more obvious what the output is. We can simply output a circular list of vertices on the boundary of the polygon. But how do we represent a polyhedron? Well, we can represent it as a list of triangular faces. A non-triangular face can always be divided into triangles, so this requirement isn't limiting.
In the 2D case, there are some degenerate cases that are easy to miss if you're not careful. For example, if there are 3 collinear points, the polygon might have two adjacent sides of the same slope, or you might combine them into one segment. Or if two points have the same $$$x$$$ coordinate, you need to handle this carefully when sorting the points by $$$x$$$ coordinate. Or if all the points are on the same line, then the convex hull isn't even a non-degenerate polygon!
Now, degenerate cases are bad enough with two dimensions. When you enter the third dimension, it only gets worse. What if four points lie on the same plane? Since we are requiring triangular faces, we could triangulate this in multiple ways. Or maybe we could choose to have one triangle of three points and the forth point lies inside this triangle, so we ignore it. What if all the points are on the same line? Or on the same plane even? Then the convex hull isn't a non-degenerate polyhedron. I will ignore such degenerate cases for now, and revisit them when applicable.
Brute Force Algorithm in $$$O(n^4)$$$
Suppose that $$$n$$$ is very small, and we are guaranteed that no four points are coplanar. Then how can we compute the 3D convex hull in the dumbest way possible?
We could simply consider every triplet of three points $$$(\vec{a}, \vec{b}, \vec{c})$$$, and check if they create a triangular face on the convex hull. In order for it to be a face, the remaining points must "see" the same side of the triangle. In other words, if we consider the plane containing this triangle, the remaining points should lie on the same side of the plane. To compute which side of a plane a point $$$\vec{p}$$$ is on, we can first take a vector $$$\vec{q}=(\vec{b}-\vec{a})\times (\vec{c}-\vec{a})$$$ orthogonal to the plane.
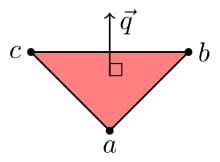
Then the sign of $$$(\vec{p}-\vec{a})\cdot \vec{q}$$$ tells us the side of the plane. In particular, a result of $$$0$$$ tells us that $$$\vec{p}$$$ lies on the plane.
For each triplet, we perform this check with all points, so the total time complexity is $$$O(n^4)$$$. Because of its simplicity, this should be the approach when the constraints allow it. And by examining the brute force case, we learned how to perform the most fundamental operation in any 3D convex hull algorithm: checking which side of a plane a point is on.
Incremental Algorithm in $$$O(n^2)$$$
Now we want a more practical algorithm. The strategy of the incremental algorithm is to build the convex hull for the first $$$i$$$ points, as $$$i$$$ goes from $$$1$$$ to $$$n$$$. All we have to do is figure out how to update the convex hull in order to accommodate one new point.
Let's start by making an analogy with the 2D convex hull. Suppose we currently have the convex hull of the first $$$i-1$$$ points, and we wish to add the $$$i$$$-th point. Well, if the point is already inside the hull, we should do nothing. Otherwise, let's pretend we are looking at the polygon from the perspective of the $$$i$$$-th point. We should delete all line segments it can see, and add two new line segments: one from the new point to each of the extreme points.
A similar thing happens in the 3D case. If a point is already inside the polyhedron, we simply do nothing. Otherwise, we delete all faces the new point can see. But what's less obvious is what we should add. Well, we've left the polyhedron with a connected set of faces removed. This exposes a cycle of edges. For each of these exposed edges, we should create a new face with the new point and that edge. Effectively, we create a cone of faces to repair the opening.
Now, let's analyze the time complexity. For each iteration, we process all faces of the hull in that iteration. And it can be proven that the number of faces is at most $$$O(n)$$$. For the proof, we use Euler's Formula. It states that for any polyhedron with $$$V$$$ vertices, $$$E$$$ edges, and $$$F$$$ faces, $$$V-E+F=2$$$. All faces are triangles, so we can substitute $$$E=3F/2$$$ since each face has $$$3$$$ edges, and we count each edge twice for the $$$2$$$ faces it touches. Then we have $$$V-F/2=2$$$ and $$$F=2V-4=O(n)$$$. Since we process $$$O(n)$$$ faces in $$$O(n)$$$ iterations, the overall time complexity is $$$O(n^2)$$$.
Clarkson-Shor Algorithm in $$$O(n\log n)$$$
There exist deterministic algorithms to compute the 3D convex hull in $$$O(n\log n)$$$ time. Most famously, there is a divide-and-conquer algorithm that solves it, but it is notoriously difficult to implement correctly. But don't lose hope! There is also a randomized algorithm based on the same incremental strategy, which takes $$$O(n\log n)$$$ time in expectation if the points are added in random order.
Unfortunately, we can't just shuffle the points, run the usual incremental algorithm, and call it a day. In order to achieve $$$O(n\log n)$$$, we should eliminate extra work of processing faces invisible to the new point. How can we do this? Well, before we checked for each point, which faces it can see. Instead, we will maintain for each point a list of faces it can see. Then when a face is created, we add it to the lists of all points that will be able to see it.
"Wait a minute," I hear you ask, "isn't this still $$$O(n^2)$$$ because you still process the same thing for each face-point pair, just in a different order?" The answer is yes, we're still in $$$O(n^2)$$$ territory. But, using some cleverness we can avoid checking with every future point every time. The key idea is that a new face $$$F$$$ is attached to a preexisting edge $$$e$$$, and a point $$$p$$$ can see $$$F$$$ only if it was able to see one of the two faces of $$$e$$$. Instead of checking with all future points, we will only check the points in the lists associated with these two faces. Unfortunately, this requires more work to implement. This time, we need to start caring about how the faces touch each other in order to find these two lists. Alternatively, we can probably do $$$O(n\log^2 n)$$$ much easier.
Precision Errors and Degenerate Cases
The only potential source for precision error is our check of which side of a plane a point is on. If all coordinates are integers, then our computations will stay as integers, so we can set an epsilon of $$$0.5$$$ and call it a day. Otherwise, if the coordinates are at most $$$X,Y,Z$$$ in absolute value (in the $$$x$$$, $$$y$$$, and $$$z$$$ directions, respectively), our computations are on the order of $$$XYZ$$$. If it's too large, we should work with floating points or bignums. If the given coordinates aren't integers, try every possible epsilon until it works try something on the order of $$$\epsilon=XYZ\cdot 10^{-k}$$$, if the mantissa of your floating-point type stores $$$k$$$ decimal digits. Whether this works may depend on which god you pray to.





