Catalan Numbers is a well known sequence of integers that appear in combinatorics, there is a chance that you might have run into such counting problems and you might have even solved them with DP without realizing that they are a known sequence. Here are a few problems to get us started.
Find the count of different binary trees with $$$n$$$ nodes, we'll denote to that by $$$C_n$$$. This can be solved by observing the substructure of the problem:
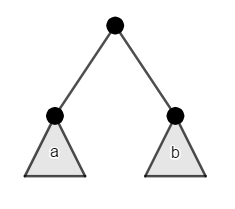
From the root, the left subtree $$$a$$$ can be any binary tree of length $$$x$$$, the right subtree $$$b$$$ can be any binary tree of length $$$y$$$, such that $$$x+y=n-1$$$. With the base case at $$$C_0=1$$$ as the empty tree is a valid tree of size $$$n$$$. This directly gives us the answer by the following recurrence relation: (Segner's recurrence relation) $$$C_{n+1} = \sum_{i=0}^{n}{C_i C_{n-i}}, n \geq 0; C_0=1$$$
The sequence of numbers $$$C_0, C_1, C_2, ...$$$ is called Catalan Numbers, and for reference they are: $$$1, 1, 2, 5, 14, 42, ...$$$






