Продолжаю свой виртуальный тур по давно минувшим раундам, в которых я не учавствовал. Моя сегодняшняя проблема это 1355D - Игра с массивом, решение которой я просто угадал 106629350. В ней не сложно понять как нужно строить массив так, что бы Петя всегда выигрывал при $$$S \geqslant 2N$$$. Доказать же, что это невозможно при $$$S < 2N$$$ гораздо сложнее. На мой взгляд доказательство, предоставленное DishonoredRighteous заслуживает подробного изучения.
Изначально у нас имеется массив $$$A$$$, состоящий из $$$N$$$ элементов. Этот массив дублируется $$$2K$$$ раз

и из него строится массив префиксных сумм $$$B$$$ размером $$$2KN$$$. В нем $$$b_0 = 0$$$ и $$$b_j = b_{j - 1} + a_j$$$ для любого $$$j > 0$$$. То есть $$$b_1 = a_1$$$, $$$b_2 = a_1 + a_2$$$, $$$b_3 = a_1 + a_2 + a_3$$$ и так далее.
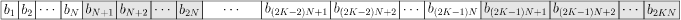
Очевидно, что в таком массиве префиксных сумм всегда выполняется равенство $$$b_{j + N} = b_j + S$$$, a последний элемент массива $$$b_{2KN} = 2KS$$$. Заметьте также, что каждый элемент массива $$$B$$$ уникален потому, что все элементы $$$A$$$ положительны.
Теперь создадим еще один массив, уже третий, назовем его $$$C$$$, и выпишем в нем все числа от $$$1$$$ до $$$2KS$$$. Разобьем его на группы размером $$$K$$$, всего таких групп получается $$$2S$$$, и раскрасим их попеременно зеленым и синим цветом.
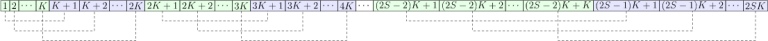
Соединим пунктирными линиями все пары чисел вида $$$X$$$ и $$$X + K$$$ у которых $$$X$$$ находится в зеленой группе. Таким образом у нас получилось $$$KS$$$ вилок между одним зеленым числом и одним синим числом.
Если в массиве $$$B$$$ есть хотя бы одна пара таких чисел, соединенных вилкой, то это означает, что разность префиксных сумм между ними, равна $$$K$$$. А это, в свою очередь, означает, что в зацикленном $$$A$$$ есть диапазон индексов $$$l$$$, $$$r$$$ такой, что $$$\sum{a_j[l \leqslant j < r]} = K$$$, причем ширина этого диапазона не превышает $$$N$$$ потому, что $$$K \leqslant S$$$ и сумма $$$N$$$ элементов изначального массива $$$A$$$ равняется $$$S$$$.
Что мы теперь имеем? В массиве $$$B$$$ у нас есть $$$2KN$$$ уникальных чисел в диапазоне от $$$1$$$ до $$$2KS$$$ включительно. В массиве $$$C$$$ у нас имеется $$$KS$$$ пар несовместимых префиксных сумм. Если $$$S < 2N$$$, то получается, что $$$KS < 2KN$$$, а это означает, что для всех чисел из массива $$$B$$$ просто не хватает свободных мест в массиве $$$C$$$. Отсюда вытекает, что если взять каждое число из $$$B$$$ и вычеркнуть его из массива $$$C$$$, то среди вычеркнутых чисел обязательно найдется пара, соединенная вилкой ($$$X$$$, $$$X + K$$$), что ведет нас к заключению о том, что в зацикленном массиве $$$A$$$ обязательно найдется непрерывный диапазон чисел с суммой $$$K$$$.
Весь трюк доказательства заключается в том, что оперируя только изначальным массивом $$$A$$$ размера $$$N$$$, доказать ничего не получается потому, что $$$K$$$ не обязательно делит $$$S$$$. Зато все прекрасно доказывается через принцип Дирихле при переходе к диапазону значений сумм кратному одновременно $$$S$$$ и $$$2K$$$.





