Hello, Codeforces!
A few days ago MohammadParsaElahimanesh posted a blog titled Can we find each Required node in segment tree in O(1)?. Apparently what they meant was to find each node in $$$\mathcal{O}(ans)$$$, according to ecnerwala's explanation. But I was too dumb to realize that and accidentally invented a parallel node resolution method, which speeds up segment tree a lot.
A benchmark for you first, with 30 million RMQ on a 32-bit integer array of 17 million elements. It was run in custom test on Codeforces on Apr 6, 2021.
- Classic implementation from cp-algorithms: 7.765 seconds, or 260 ns per query
- Optimized classic implementation: (which I was taught) 4.452 seconds, or 150 ns per query (75% faster than classic)
- Bottom-up implementation: 1.914 seconds, or 64 ns per query (133% faster than optimized)
- Novel parallel implementation: 0.383 seconds, or 13 ns per query (400% faster than bottom-up, or 2000% faster than classic implementation) ## FAQ
Q: Is it really that fast? Idk, try it. Looks fast to me.
Q: Why? Maybe you want your $$$\mathcal{O}(n \log^2 n)$$$ solution to pass in a problem with $$$\mathcal{O}(n \log n)$$$ model solution. Maybe you want to troll problemsetters. Maybe you want to obfuscate your code so that no one would understand you used a segment tree so that no one hacks you (just kidding, you'll get FST anyway). Choose an excuse for yourself. I want contribution too.
Q: License? Tough question because we're in CP. So you may use it under MIT license for competitive programming, e.g. on Codeforces, and under GPLv3 otherwise.
Q: Any pitfalls? Yes, sadly. It requires AVX2 instructions which are supported on Codeforces, but may not be supported on other judges.
How it works
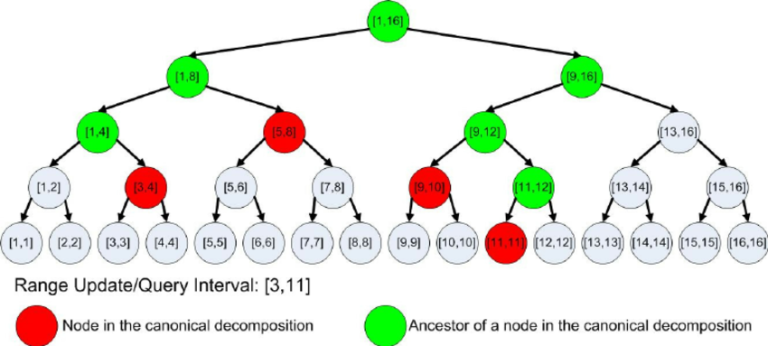
A range query is decomposed into red nodes. Classic segment tree implementations don't find these red nodes directly, but execute recursively on green nodes. Bottom-up segment tree implementation does enumerate these nodes directly, but it also enumerates a few other unused nodes.
The parallel implementation accesses






