Hello, codeforces.
I think this technique is important, and easy to code, although I haven't found much about it, so I've decided to make a blog explaining it.This technique allows to compare substrings lexicographically in $$$O (1)$$$ with a preprocessing in $$$O (NlogN)$$$.
As this is my first post on codeforces, please let me know if there are any mistakes.
Prerequisites:
- Basic strings knowledge.
- Sparse Table(Optional).
What is a Dictionary of Basic Factors?
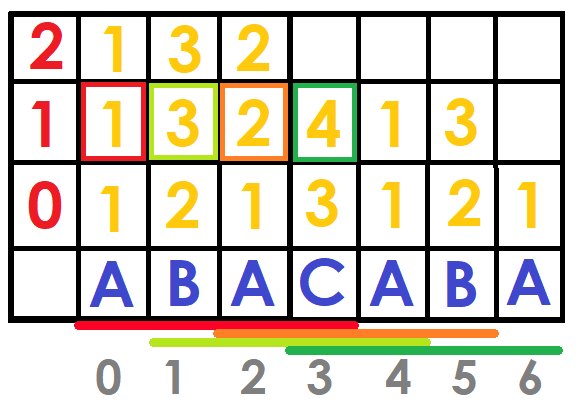
As in the sparse table we will have a matrix of size $$$N\log{N}$$$ called $$$DFB$$$, where $$$DFB[i][j]$$$ tells us the position of the string $$$S[i ... i + 2^j-1]$$$ (the first time it appears) among all the strings of size $$$2^j$$$ ordered lexicographically.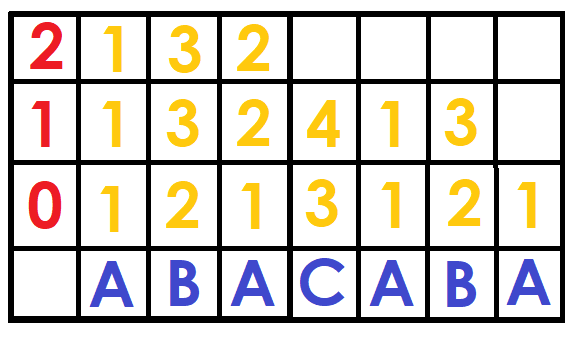
So, how do we build the matrix? Let's start with the lowest level, for powers of size $$$2^0$$$, we simply put the position of the character $$$S[i]$$$ in the dictionary (1 for 'A', 2 for 'B' ... and so on).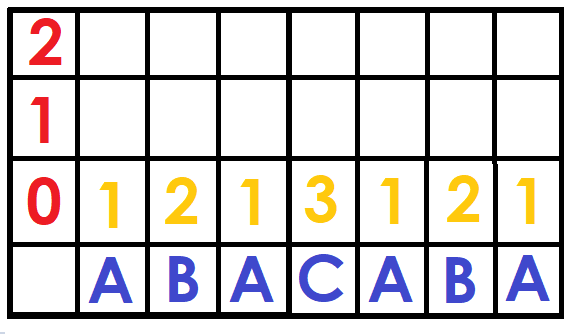
For the following $$$ DFB[i][j] $$$ we can save a pair of numbers that are $$$(DFB[i][j-1], DFB[i+2^{j-1}][j-1]) $$$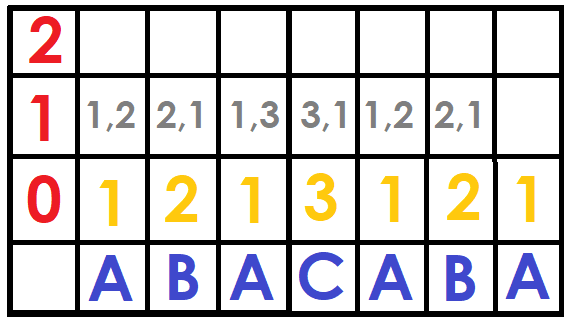
Now we replace the pairs by their position (the first time the pair appears) on the ordered array of those pairs, this can be done with Counting Sort in $$$O(N)$$$ (I'll explain it more deeply later), otherwise with a normal sort in $$$O(NlogN)$$$ (But this will slow down the algorithm).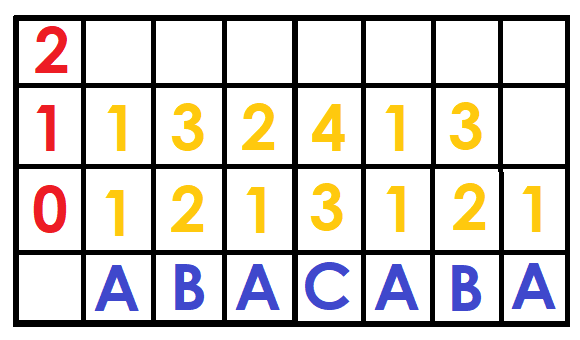
We do that for all powers of two and we will have the complete matrix.
Handling queries:
Suppose we want to make a query that is "Say which of the two substrings $$$S[l_{1}...r_{1}]$$$ and $$$S[l_{2}...r_{2}]$$$ is smaller lexicographically?".
First of all, let's analyze that if the substrings have different sizes, we can compare only the prefixes of size $$$M$$$ where $$$M$$$ is the minimum size between the two substrings, if both prefixes are equal then the smallest lexicographically is the substring of smaller size.
As in the Sparse Table, suppose $$$ k = \ log {(r-l)} $$$, then we can represent the substring $$$ S [l ... r] $$$ as the pair $$$ ( DBF [l] [k], DFB [r-2^k+1] [k] ) $$$. Now to compare two substrings of equal size we simply lexicographically compare their pairs in $$$O(1)$$$.
For example, suppose we have the string "ABACABA" and we want to know which string is lexicographically smaller between $$$ S [0 ... 5] $$$ and $$$ S [1 ... 6] $$$ ("ABACAB" and "BACABA").Since $$$\log{(5-0)}=2$$$, the pairs to compare would be: $$$(DBF [0] [2], DBF [2] [2])$$$ and $$$(DBF [1] [2], DBF [2] [2])$$$, which would be $$$(1,2)$$$ and $$$(2,4)$$$ therefore the first substring is lexicographically smaller.