Hi codeforces! I was trying to learn about Li-Chao tree by some blog which i can find on gg (codeforces included). But there still some issue i was encountered while I trying to understood Li-Chao tree. Fortunately! I found that there's a simpler way to understand LC tree by thinking about another approach. So, I decide to write this blog for two reason :
Archive
Sharing
If you feel interesting about this topic, welcome!
Prerequisite :
Did you read one of two blog ? :
I.Which issue that me (or maybe someone) stuck in Li-Chao tree?
These question are main motivation :
- Why node on $$$Li-Chao$$$ $$$tree$$$ only store one line that is $$$min/max$$$ at point $$$mid$$$ which $$$mid$$$ is the point middle in segment $$$[L, R]$$$ which current node manage?
- Why in $$$Query$$$ function we get $$$max$$$ result on way from root to leaf instead of get a value in node which include point we want to query?
I guess that somebody maybe stuck in here, so, we will answer it later.
II.Problemstatement
You must give a data structure which can do two following operation by the best way you can :
Add a line $$$y = a*x + b$$$ into set $$$S$$$
Given a point $$$x$$$, find $$$min$$$ value of $$$y$$$ among all line we added
Similar to $$$Li-Chao$$$ $$$tree$$$, we manage convex hull by the way maintain a segment $$$[L, R]$$$, for each intergers $$$x$$$ in $$$[L, R]$$$ we store line $$$y = a*x + b$$$ such that the line $$$y = a*x + b$$$ reach min at point with coordinate $$$x$$$.
Add operation : We can see that we will only care about convex hull of $$$S$$$, so that we will maintain it.
We can reach two observation :
Add two line $$$x =\infty$$$ and $$$x = +\infty$$$ into $$$S$$$. Easy to see that the convex hull look like a parabol with nagative slope.
If a line lie on convex hull, it will lie on a continuous interval on convex hull.
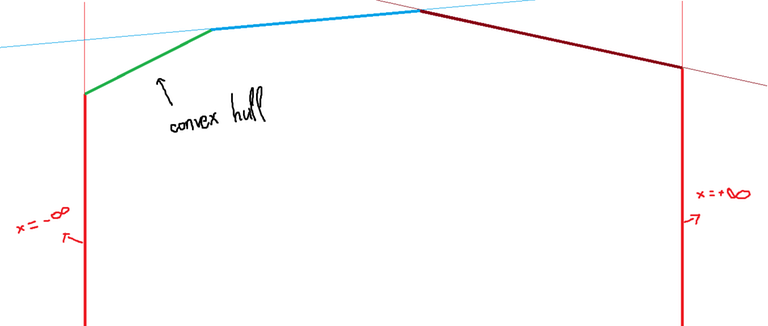
Thicker line represent the convex hull
We can iterate over [L, R] whenever we add a new line into S to update the "min line" for each point in $$$[L, R]$$$
However, by two observation above, we can do ternary search to find point x such that:
$$$x$$$ $$$\in$$$ $$$[L, R]$$$
At $$$x$$$ coordinate, the current line $$$y = a*x + b$$$ is the "min line".





