Hello Codeforces!

I'm glad to write a tutorial post again after several years (you can find old tutorials in my blog posts). I'm here to present an implementation for an algorithm that calculates inclusion hierarchy among circles. The main article can be found here. The repository where the implementation can be found is here. If you want to play, it has a python GUI too.

The problem

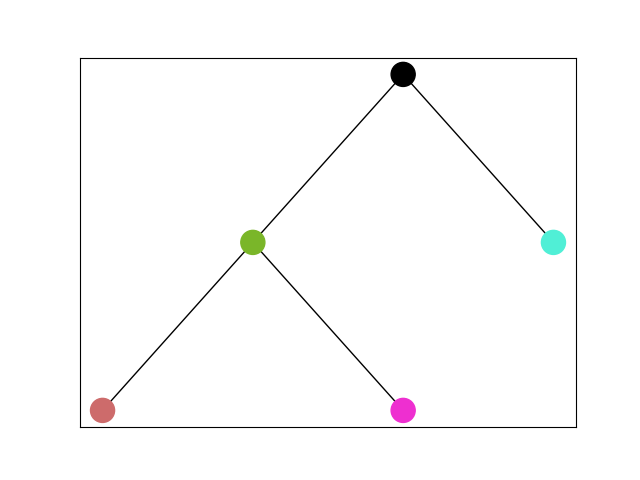
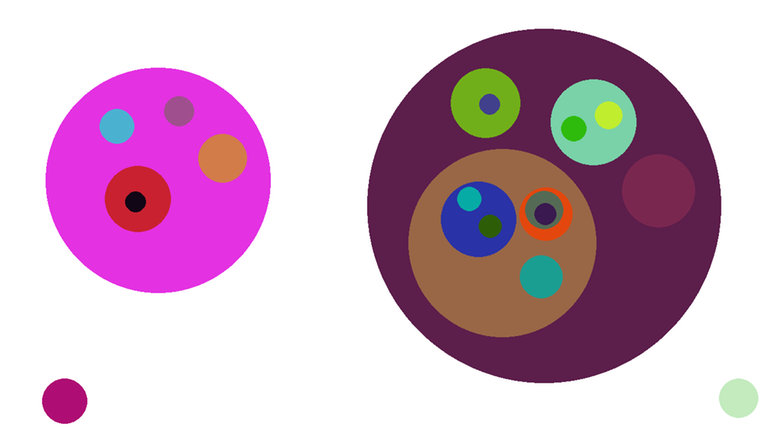
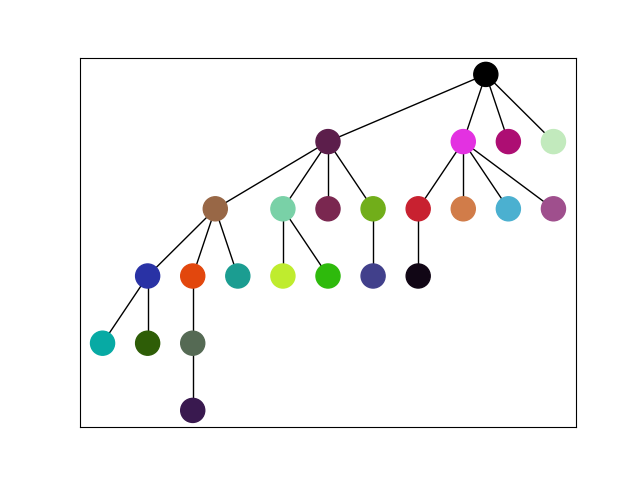
Consider $$$n$$$ non-intersecting circles. Some circles can be inside of others. We need to make a tree of these $$$n$$$ circles such that if $$$i$$$-th circle is inside of $$$j$$$-th circle, the $$$i$$$-th vertex be in the subtree of $$$j$$$-th vertex. For example:

The black vertex is the whole surface itself.

Algorithm description summary

Move the sweep-line from left to right. At each $$$x$$$, the sweep-line intersects with some circles in some segments of $$$y$$$. These segments are non-intersecting but some of them could be inside of other ones. We need to dynamically keep the order of these segments in our set (e.g. std::set in C++) and when sweep-line sees a new circle, we can find the parent of this circle in the set using a binary search (lower_bound in C++).

Time complexity is $$$\mathcal{O}(n \log n)$$$. You can find the details in the main article or the implementation.

This was my Bachelor's project, you can see the full project here.