103503A — Make Sum Great Again
Author: Gheal
It is always optimal to add the smallest integer which is not already in the array.
The number of operations will never exceed √2⋅s.
Based on the first hint, the final array will be equal to v1,v1,…,vn∪[1,x], for some x.
Hint 4: How can we find the value of x faster than O(√s)?
Lemma: The number of operations will never exceed √2⋅s.
Since we need to maximize the final length of the array, it is always optimal to add the smallest integer which is not already present in a.
The naive implementation of this idea has a runtime complexity of O(n⋅√s), although this can be easily optimized to O((n+√s)log(n)), if binary search is used to check whether the new elements are already present in a.
The optimal solution has a runtime complexity of O(NlogS). Based on hints 3 and 4, we can find the value of x with binary search. For some x, the sum of the elements in a will be equal to sum(x)=x⋅(x+1)2+∑1vi, where ∑1vi is the sum of the elements greater than x.
Since the sum of elements sum(x) is a monotonous function, we can use binary search on the interval [1,√2⋅s] to find the exact value of x.
Final time complexity: O(NlogS)
103503B — Binary Search Search
Author: Gheal
The numbers are printed in ``layers''.
Try to represent the layers as a binary tree.
To better understand the solution, let's consider n=12. The final array is the BFS traversal starting from the root of the following binary tree:
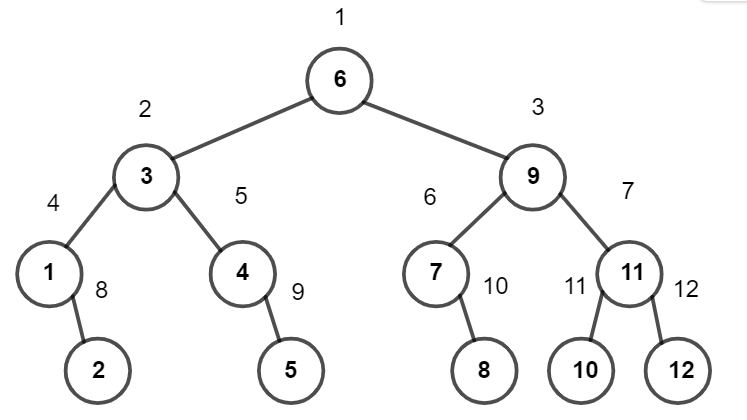
This binary tree was generated by starting with the root m=⌊n+12⌋=6. Each node m=⌊l+r2⌋ has up to two children: m1=⌊l+(m−1)2⌋ and m2=⌊r+(m+1)2⌋.
If our given integer k is in a complete layer, then we can employ a binary search-type algorithm to find the position of k:
l = 1, r = n, position = 1, visited_nodes = 1
while(visited_nodes<=n){
m = (l + r) / 2
if(k==m){
print position
return
}
if(k<m) position = position * 2
else position = position * 2 + 1
visited_nodes = visited_nodes * 2 + 1
}This algorithm has the added benefit of not printing anything if k is not in a complete layer. In this case, the position of k in the last layer can be determined from position, although this isn't very straightforward. If the binary tree were complete, then the position of k in the last layer would be position−visited_nodes−12, since there are visited_nodes−12 nodes on the other layers, all of which will be printed before k.
By looking at the missing nodes from the binary tree for n=12, one may make the crucial observation that the general case position for k in the last layer is equal to k−(position−visited_nodes−12).
In conclusion, the final position for k will be k−(position−visited_nodes−12)+visited_nodes−12=k+visited_nodes−position−1.
Time complexity per testcase: O(logn)
103503C — Plates
Author: Gheal
Any final configuration can be uniquely determined by a permutation of 1,2,3,…,k
k≤20
Let dp[mask] be the minimum number of moves required to cover the first Σki=1getBit(mask,i)∗pi slots with all plates of colours c1,c2,… where getBit(mask,ci)=1,∀i. Naturally, dp[0]=0.
Transitioning from dp[mask] to dp[mask+2k], where getBit(mask,k)=0 can be done fairly easily. Let pos=Σki=1getBit(mask,i)∗pi and cntdiff(l,r,k) be the number of plates in the initial configuration ai which satisfy the following requirements:
- l≤i≤r;
- ai≠0;
- \neq k$.
From these definitions, the value of dp[mask+2k] can be computed using the following formula:
cntdiff(l,r,k) can be calculated in O(1) per query using prefix sums. Calculating the prefix sums has a time complexity of O(n⋅k).
Intended time complexity: O(n⋅k+2k⋅k)
Reconstructing the final configuration will also require an auxiliary array prev[mask] — the last colour added to mask.





