CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
32:35:26
Зарегистрироваться »
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Hello, Codeforces!
Zlobober and I are glad to invite you to compete in Nebius Welcome Round (Div. 1 + Div. 2) that will start on 12.03.2023 17:35 (Московское время). The round will be rated for everyone and will feature 8 problems that you will have 2 hours to solve.
I feel really thrilled and excited about this round as this is the first time I put so much effort in a Codeforces contest since I quit being a round coordinator in December 2016 (wow, that was so long ago)!
We conduct this round to have some fun and we also hope to find some great candidates to join Nebius team. Solving 5+ problems in our round will be a good result and will count as one of the coding interviews. Apart from that top 25 contestants and 25 random contestants placed 26-200 will receive a branded Nebius t-shirt!

Some information about Nebius. I have joined this new start-up in cloud technologies in November as a head of Compute & Network Services. It's an international spin-off of Yandex cloud business with offices in Amsterdam, Belgrade and Tel Aviv. We offer strategic partnerships to leading companies around the world, empowering them to create their own local cloud hyperscaler platforms and become trustworthy providers of cloud services and technologies in their own regions.
We know that competitive programming makes great engineers. It boosts your algorithms and coding skills, teaches you to write a working and efficient code. We aim to hire a lot of backend software engineers for all parts of our cloud technology stack that ranges from hypervisor and network to data warehouse and machine learning.
Here you can check Nebius website and open positions. If you feel interested in joining Nebius as a full-time employee, go on and fill the form.
Special thanks go to:
MikeMirzayanov for his outstanding, glorious, terrific (you can't say enough, really) platforms Codeforces and Polygon
74TrAkToR and KAN for this round coordination (and for rounds coordination in general, good job lads!)
ch_egor for his help with one of the problem that has a peculiar setting which we will discuss a lot in the editorial
UPD Now that the list is complete we can say many thanks to all the testers! dario2994, errorgorn, magga, golikovnik, Hyperbolic, Farhan132, IgorI, vintage_Vlad_Makeev, aymanrs, Vladik, Junco_dh, dshindov, csegura, Eddard, Alexdat2000, kLOLik, wuruzhao, Aleks5d, Ryougi-Shiki, qrort, ak2006, AsGreyWolf, farmerboy, vladukha, usernameson, segment_tea, DzumDzum, Java, samvel, qwexd, Tensei8869, thank you for all your help on improving this round's quality!
Fingers crossed all will be well, you will enjoy the round and we will be back with a new one in several months!
UPD2 The scoring distribution is 500 — 1000 — 1000 — 1500 — 2000 — 2750 — 3500 — 3500.
UPD3 The editorial is here!
UPD4 Congratulations to winners!
1-st place: jiangly
2-nd place: tourist
3-rd place: Um_nik
4-th place: isaf27
5-th place: Ormlis
UPD5 T-shirts winners!
TL;DR Летние стажировки — это классно, просто поверьте. Ссылка, если хотите попасть на летнюю стажировку в Яндекс.
Всем привет!
С недавнего времени я стал разработчиком компании Яндекс, и никак не мог пройти мимо просьбы рассказать на Codeforces про нашу программу летних стажировок. За время учёбы на специалитете МГУ и в аспирантуре НИУ ВШЭ, у меня было пять стажировок, которые проходили в четырёх разных странах и трёх IT-компаниях (одна из компаний -- Яндекс, угадайте другие две), поэтому всё нижесказанное основано исключительно на личном опыте, и опыте моих друзей-стажёров.
Итак, почему я совершенно искренне считаю, что летняя стажировка в крупной IT-компании — это самый лучший из всех испробованных мной способов провести лето.
Опыт разработки промышленного кода для решения каких-то реально существующих задач. Наверняка, многие из вас, будучи опытными олимпиадниками, которые немало задач в своей жизни сдали с чистого плюсика, периодически задавали себе такие вопросы как "Ну неужели нельзя просто написать код, чтобы он сразу хорошо и быстро работал, какие тут вообще могут быть проблемы?" и "Господи, ну как можно было допустить ТАКОЙ баг?". Что же, могу вам пообещать, что первое же знакомство с миром промышленного программированию развеет добрую половину подобных иллюзий, вы поймёте, какие трудности таятся в проектировании и поддержке кода, как непросто бывает обеспечить качественное тестирование и взаимодействие нескольких сложных систем, и почему иногда самые эффективные промышленные решения могут быть похожи на костыль от взломанного на раунде участника.
Ценный жизненный опыт. С точки зрения жизненного опыта особенно хороши летние стажировки, так как летом можно забыть об учёбе и по-настоящему погрузиться во "взрослую" жизнь разработчика. Для достижения ultimate-эффекта рекомендую отправляться на стажировку в другой город, особенно если вы не переезжали ради учёбы. Ходить каждый день на работу, взаимодействовать с коллегами и начальником, посещать рабочие встречи, получать (и, конечно, тратить) зарплату. Кому-то может показаться, что в этих вопросах нет никаких особенностей и подводных камней, мир вокруг справедлив, а люди приятные и адекватные by design. Подсказка: нет, это так только если вы сразу оказались в правильном месте.
Новый коллектив. Скорее всего люди, с которыми вы провзаимодействуете за время стажировки, будут существенно отличаться от людей, с которыми вы ежедневно общаетесь сейчас, а значит знакомство с ними поможет вам сильно расширить свой кругозор и представление об окружающим мире. Совет: никогда не отвечайте "нет, в другой раз" на приглашение малознакомых коллег пообедать вместе, ваши чатики в телеграмме никуда не убегут, в отличие от клёвых историй, рассказанных за такими обедами :)
Ещё раз ссылка на страницу программы, для тех, кого я смог убедить. Если же я смог убедить вас только наполовину, то рекомендую посмотреть трансляцию встречи Лето в Яндексе (к сожалению, я слишком поздно пишу этот пост, чтобы предложить на неё сходить), которая пройдёт в ближайший четверг, 21 февраля, начало в 15:00 (программа выступлений).
Интеллектуальный вендинг
Автор идеи и разработчик: GlebsHP.
Заметим, что в любом случае Аркадий не может потратить больше денег, чем у него есть, поэтому количество купленных бутылок не превзойдёт 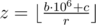 . Однако, может так получится, что Аркадию придётся купить меньше бутылок, если в какой-то момент у Аркадия не будет хватать мелочи на покупку без сдачи, а нужно количество сдачи в автомате не будет.
. Однако, может так получится, что Аркадию придётся купить меньше бутылок, если в какой-то момент у Аркадия не будет хватать мелочи на покупку без сдачи, а нужно количество сдачи в автомате не будет.
Заметим, что суммарное количество мелочи в обороте не меняется и составляет c + d. При этом, если c + d ≥ 999 999, то либо у Аркадия всегда найдётся мелочь, чтобы купить очередную бутылку, либо автомат сможет дать сдачу, если платить только с помощью банкнот. В этом случае ответ равен z.
Если же c + d < 999 999, то может быть, что у Аркадия хватает мелочи для совершения покупки без сдачи, может быть, что в автомате достаточно сдачи для покупки банкнотами, но не может быть одновременно выполнено и то и другое, а значит, действия Аркадия определяются однозначно. В этом случае можно было бы промоделировать его действия, однако, их может оказаться слишком много.
Обозначим через ai количество монет у Аркадия после первых i действий (то есть a0 = c). Заметим, что если ai = aj, то ai + 1 = aj + 1 (действительно, следующее действие однозначно определяется величиной ai), а значит последовательность зацикливается и повторяется. Будем моделировать действия Аркадия по покупке бутылок напитка Квас-Класс, до тех пор пока какое-то из значений ai не повторится, либо не возникнет ситуация, когда Аркадий не может совершить следующую покупку. В случае повторения значения ai в качестве ответа выведем величину z, в противном случае номер итерации, на котором не получилось совершить очередную покупку.
Упражнение: придумайте решение задачи, если все банкноты имеют номинал 1012.
НВП против НУП
Автор идеи и разработчик: Endagorion.
Нарисуем на плоскости n точек pi = (i, ai). Пусть I = (i1, ..., ik) и J = (j1, ..., jl)~--- пара непересекающихся НВП и НУП. Из максимальности I следует, что строго внутри следующих прямоугольников не содержится точек (прямоугольники описываем координатами противоположных углов):
A0 = ((0, 0), pi1);
Ax = (pix, pix + 1) для всех 1 ≤ x < k;
Ak = (pik, (n + 1, n + 1)).
Аналогично, поскольку J максимальна, не может быть точек в следующих прямоугольниках:
B0 = ((0, n + 1), pj1);
By = (pjy, pjy + 1) для всех 1 ≤ y < l;
Bl = (pjl, (n + 1, 0)).
Эти две цепочки прямоугольников соединяют пары противоположных углов квадрата ((0, 0), (n + 1, n + 1)). В предположении, что I и J не пересекаются, у нас обязательно дожна быть пара пересекающихся прямоугольников Ax и By. Поскольку никакие прямоугольники Ax и By не содержат точек, есть всего два случая, как они могут пересечься:
ix < jy < jy + 1 < ix + 1, ajy + 1 < aix < aix + 1 < ajy (как в первом примере);
jy < ix < ix + 1 < jy + 1, aix < ajy + 1 < ajy < aix + 1 (зеркальное отражение предыдущего).
Поищем пересечения типа 1 (для типа 2 перевернем перестановку и поищем еще раз). Скажем, что (i, i') является {\it НВП-парой}, если a и b являются последовательными элементами в какой-то НВП (аналогично определим {\it НУП-пару}). Пускай существуют НВП-пара (i, i') и НУП-пара (j, j'), удовлетворяющие i < j < j' < i' и aj' < ai < ai' < aj, то есть какие-то НВП и НУП имеют пересечение типа 1. Это означает, что ответ можно найти, построив все НВП- и НУП-пары и поискав такое пересечение.
Конечно, всевозможных пар слишком много. Однако, заметим, что в ситуации выше мы можем заменить i' на  , а j' на
, а j' на  . Поэтому можно оставить в рассмотрении O(n) пар. Пересечения среди них поищем сканирующей прямой с деревом отрезков.
. Поэтому можно оставить в рассмотрении O(n) пар. Пересечения среди них поищем сканирующей прямой с деревом отрезков.
Прогулки за едой
Автор идеи и разработчик: GlebsHP.
Сначала решим версию задачи, в которой изначальное перемещение совершается бесплатно, а после x съеденных единиц еды перемещение на 1 стоит x. Несложно видеть, что оптимальной стратегией будет дойти до какой-то позиции k, а затем двигаться только в сторону позиции 0, заходя в какие-то рестораны. Пусть мы зашли в ресторан i, тогда вес увеличился на ai и каждое перемещение также стало на ai дороже. Поскольку в оптимальной стратегии мы посещаем рестораны только двигаясь в сторону позиции 0, то можно сразу сказать, что посещение ресторана i в итоге обойдётся в ai·i единиц энергии.
Получаем задачу о рюкзаке, есть n предметов, i-й из них имеет вес ai·i и стоимость ai, требуется выбрать подмножество предметов с максимальной суммарной стоимостью и весом не более e. Стандартный способ решения такой задачи предполагает использовать динамическое программирование d(i, x) — максимально возможная суммарная стоимость, если из первых i предметов набрать подмножество веса x.
Произведём замену параметра, будем вычислять динамическое программирование d(i, c) — минимально возможный вес, если из первых i предметов выбрать подмножество суммарного веса c. Далее, будем добавлять предметы в порядке уменьшения значения i, то есть для получения d(i, c) можно использовать только рестораны с i-го по n-й. Какие значения параметра c имеет смысл рассматривать? Любая единица стоимости (то есть насыщения в терминах исходной задачи), полученная в ресторанах с номерами ≥ i требует затрат хотя бы i единиц энергии, поэтому имеет смысл рассматривать только 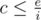 . Воспользуемся формулами оценки суммы гармонического ряда и получим, что количество значений динамического программирования, которые нам требуется вычислить оценивается как
. Воспользуемся формулами оценки суммы гармонического ряда и получим, что количество значений динамического программирования, которые нам требуется вычислить оценивается как 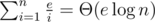 .
.
Последним штрихом будет учесть исходную стоимость перемещения до позиции, где будет посещён ресторан с наибольшим индексом. Пусть эта будет ресторан k, тогда к ответу требуется прибавить 2k, что можно учесть в момент перехода из состояния d(i, 0) при вычислении значений динамического программирования.
Поисковик
Автор идеи: GlebsHP, разработка задачи: cdkrot.
Для начала заметим, что в конце, после приписывания всех букв, Алиса получит в точности строку s.
Действительно, пусть мы приписывали буквы, и оставались внутри строки, а потом после некоторого приписывания все вхождения пропали. Тогда все дальнейшие приписывания не увеличивают итоговую сумму, а вместо этого можно было бы выделить на том роковом шаге одно из вхождений, и просто растить слово влево и вправо до границ s.
Воспользуемся этим знанием, чтобы решить задачу. В частности, можно развернуть процесс: скажем, что нам изначальна дана строка s, а затем из неё постепенно выкидывают буквы слева или справа.
Построим по строке суффиксное дерево, то есть бор, в который добавили все суффиксы строки s.
Будем делать динамику от вершины — dp[v] = максимальной сумме, которую можно получить, если начать со строки, соответствующей пути от корня до v и выкидывать буквы с краёв, считая сумму вхождений по всей большой строке s.
В этой динамике всего два перехода — можно подняться в предка (что соответствует выкидыванию буквы справа), или перейти по суффиксной ссылке (что соответствует выкидыванию буквы слева). Считать динамику можно лениво, а количество вхождений~--- это количество терминальных вершин в поддереве (что можно предподсчитать заранее для всех вершин).
Правда, чтобы в динамике было меньше n2 состояний, придётся перейти к сжатому суфдереву.
В таком случае, переход в предка может соответствовать выкидыванию сразу нескольких букв справа, в таком случае посередине этого ребра количество вхождений совпадает с количеством вхождений у нижнего конца ребра. Аналогично дела обстоят и с суффиксной ссылкой.
Единственное что мы не учли, так это то, что возможно в оптимальном ответе переходы наверх по ребру и по суффиксной ссылке "перемешаны", и из-за сжатия суфдерева мы таких переходов не увидим. На самом деле это ничего не портит. Действительно, если мы поднимались по длинном ребру, сделали переход по суфссылке и доподнимались по ребру, то можно было сразу пойти по суфссылке, а уж затем подниматься по ребру — количество вхождений от такой перестановки может только увеличится.
Асимптотика решения — 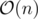 , задачу можно также решить с помощью суффиксного автомата и динамики на нём, в таком случае переходами динамики тоже являются суффиксные ссылки и обратные рёбра.
, задачу можно также решить с помощью суффиксного автомата и динамики на нём, в таком случае переходами динамики тоже являются суффиксные ссылки и обратные рёбра.
Упражнение: решите задачу, если в качестве стартовой строки даётся не пустая строка, а некоторая подстрока исходной строки, заданная как границы вхождения (li и ri). При этом требуется решить задачу для 100 000 различных запросов.
Угадай меня, если сможешь
Автор идеи и разработчик: GlebsHP.
Заметим, что если мы по очереди назовём все элементы в каком-нибудь порядке, то в завершении ситуация будет аналогична исходной, но со сдвигом на 1. Такой сдвиг никак не влияет ни на ответ, ни на промежуточные значения, возвращаемые интерактором.
Посмотрим на тройку элементов i, j и k, такую что pi + 1 = pj = pk - 1. В случае, если мы перечислим все элементы в таком порядке, что j будет идти раньше i и раньше k, то в момент когда pj увеличится на один, количество различных элементов уменьшится и мы сможем с уверенностью сказать, то на позиции j не находится максимум.
Выберем случайную перестановку и назовём элементы в соответствующем ей порядке. В тройке i, j, k, описанной выше, вероятность того, что j будет назван раньше i и k составляет  . Таким образом, если проделать эту операцию 50 раз, используя каждый раз новую случайную перестановку, то вероятность, что элемент j не являющийся максимумом всё ещё не будет помечен составляет лишь
. Таким образом, если проделать эту операцию 50 раз, используя каждый раз новую случайную перестановку, то вероятность, что элемент j не являющийся максимумом всё ещё не будет помечен составляет лишь 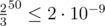 . Поскольку события выполнения для каждой тройки i, j, k нельзя назвать независимыми, то оценим вероятность ошибки хотя бы на одном элементе как 2·10 - 9·n ≤ 2·10 - 6 в указанных ограничениях.
. Поскольку события выполнения для каждой тройки i, j, k нельзя назвать независимыми, то оценим вероятность ошибки хотя бы на одном элементе как 2·10 - 9·n ≤ 2·10 - 6 в указанных ограничениях.
Хеширование для ленивых
Автор идеи GlebsHP. Разработка задачи: Arterm.
Заметим, что 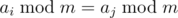 если и только если m|ai - aj. Следовательно, надо найти наименьшее m, не делящее ни одну разность чисел в данном массиве.
если и только если m|ai - aj. Следовательно, надо найти наименьшее m, не делящее ни одну разность чисел в данном массиве.
Для начала найдем все разности. Положим
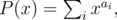
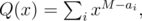
где M = max ai. Вычислим произведение T(x) = P(x)·Q(x) с помощью быстрого преобразования Фурье. Так как
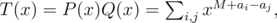
то коэффициент при xM + d ненулевой тогда и только тогда в массив a если два числа с разностью d.
Теперь для каждого m на отрезке [1, M] проверим, если ли среди разностей кратная m. Сделать это мы можем за 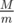 . Так мы найдем ответ на задачу за время
. Так мы найдем ответ на задачу за время 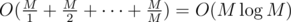 .
.
Сложность работы обоих частей 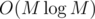 , где M = max ai ≤ 2 000 000.
, где M = max ai ≤ 2 000 000.
Привет! 19-20 мая в Яндексе в Санкт-Петербурге будет проходить финальный раунд Яндекс.Алгоритма. Мы будем очень рады видеть вас среди гостей мероприятия. Заполните форму по ссылке, чтобы мы могли спланировать всё. https://contest.yandex.ru/algorithm2018/guest/
Расписание:
19 мая, 16:30 до 19:00. Экскурсия по офису, настольные игры и приставки в офисе.
20 мая, 9:30. Регистрация.
20 мая, 10:00 — 11:00. Пробный тур.
20 мая, 11:00. Начало основного тура.
20 мая, 14:30 — 15:00. Лекция от команды поиска.
20 мая, 15:00 — 15:30. Награждение победителей.
Если вы знаете, кому еще может быть интересно такое приглашение, перешлите его и пригласите гостя заполнить форму регистрации, даже если гость не из Яндекса. Спасибо!
Если вы вдруг хотите принять участия в Яндекс.Алгоритме 2018, но по какой-то причине ещё не зарегистрировались, то стоит пройти по этой ссылке.
Квалификационный раунд соревнования стартовал в 00:00 по Москве в субботу 17 февраля. Раунд является виртуальным соревнованием продолжительностью 100 минут, начать которое можно в любой момент до 23:59 воскресенья 18 февраля (время московское).
Напоминаем, что для прохода в отборочный этап необходимо сдать хотя бы одну задачу. При этом, все участники, сдавшие хотя бы одну задачу в разминочном раунде, считаются уже прошедшими квалификацию.
Жюри настойчиво просит участников никак не обсуждать задачи не публиковать решения до 01:40 19 февраля.
Желаем успехов и надеемся, что вы получите удовольствие от процесса решения задач!
A. Время в зазеркалье
Рассмотрим движение "прямой" и "отражённой" стрелки. За то время, когда "прямая" стрелка повернётся на некоторый угол, "отражённая" повернётся на тот же угол, но в другую сторону, то есть суммарный угол поворота стрелок равен полному обороту. Для каждой стрелки независимо вычислим её позицию. Для часовой это 12 минус текущая позиция, а для минутной — 60 минус текущая позиция. В обоих случая надо не забыть заменить 12 или 60 на ноль.
B. Фактор палинромности
Пусть существует какая-то подстрока, являющаяся палиндромом. Если мы уберём первый и последний символ палиндрома, оставшаяся строка тоже будет палиндромом. Будем повторять процесс до тех пор, пока не останется строка из двух или трёх букв (в зависимости от чётности).
Подстрок длины два или три всегда линейное количество, и суммарная их длина также линейна, поэтому среди таких строк ответ можно выбрать наивным алгоритмом. Если же ни одна из подстрок такой длины не является палиндромом, то выведем - 1.
C. Разделите их все
Для решения этой задачи нам потребуется простой геометрический факт, что прямая делит окружность на две равные части если и только если она проходит через её центр. Аналогично для прямоугольника, прямая делит его на две части равной площади если и только если она проходит через точку пересечения диагоналей. В обоих случаях достаточность следует из симметрии относительно этой точки, а необходимость может быть установлена проведением через эту точку прямой, параллельной данной.
Теперь нам требуется лишь проверить, правда ли все центры заданных во входных данных фигур лежат на одной прямой. Для удобства будем рассматривать удвоенные координаты центров, тогда для получения центра прямоугольника достаточно сложить координаты двух противоположных вершин.
Если среди построенного множества точек не более двух различных, то ответ точно положительный. В противном случае рассмотрим любую пару различных точек, и проверим, что все остальные точки лежат на определяемой этой парой прямой. Наиболее удобный способ проверить, что три точки a, b и c (a ≠ b) лежат на одной прямой~--- использовать векторное произведение векторов b - a и c - a. Итоговая сложность решения: O(n).
D. Задача для собеседования
Докажем несколько лемм.
Лемма 1. Числа, оказавшиеся на каком-то шаге соседними, являются взаимно простыми.
Докажем по индукции. База очевидна (1 и 1 взаимно просты). Пусть доказано для n шагов. Все числа, выписанные на n + 1-м шаге, являются суммой двух соседних на n-м шаге чисел, то есть суммой двух взаимно простых чисел. Но НОД (a + b, b) = НОД (a,b)=1. Лемма доказана.
Лемма 2. Никакая упорядоченная пара соседних чисел (a, b) не может возникнуть в последовательности более одного раза (ни на одном шаге, ни на разных).
Пусть это не так, тогда отметим номер k шага, на котором в первый раз возникло повторение (то есть повторилась пара, существующая на этом или на предыдущем шаге). Пусть пара (p, q) возникла на k-м и на i ≤ k-м шаге. Но тогда, если p > q, то p было построено как сумма соседей q и p - q (если p < q, то q было построено как сумма p и q - p), то есть на k - 1-м и на i - 1-м шагах также существовало повторение, что противоречит нашему предположению. Лемма доказана.
Лемма 3. Любая упорядоченная пара взаимно простых чисел неизбежно будет соседней на некотором шаге.
Пусть мы имеем числа pq, стоящие рядом на некотором шаге и пусть p > q (без ограничения общности). Тогда p было получено как сумма p - q+q, то есть на предыдущем шаге рядом стояли p - q и q. Если p - q < q, то два шага назад справа от q стояло число 2q - p, если p - q > q, то слева от p - q стояло число p - 2q и так далее. Так как p и q взаимно просты, то на каком-то шаге этот процесс, по сути являющийся разновидностью алгоритма Евклида, приведёт к тому, что с одной стороны окажется 1, а с другой — некоторое натуральное число. Но пара (1, x) или (x, 1) для любого x будет соседней последовательности на x-м шаге. А так как действия восстанавливаются однозначно, то это значит, что и исходная пара (p, q) в какой-то момент встретится в качестве соседней.
Таким образом, каждая упорядоченная пара взаимно простых чисел ровно один раз встречается в качестве соседей в заданной последовательности. Поэтому задача сводится к подсчёту количества упорядоченных пар взаимно простых чисел, дающих в сумме n. Так как если p и n взаимно просты, то и p и n - p взаимно просты, то количество таких пар можно поставить в однозначное соответствие количеству чисел, взаимно простых с n, или значению функции Эйлера от n.
Подсчёт же количества таких чисел является известной задачей и опирается на мультипликативность функции Эйлера: если n = p1k1·p2k2·...·pnkn, то взаимно простых с n чисел будет (p1k1 - p1k1 - 1)·(p2k2 - p2k2 - 1)·... (pnkn - pnkn - 1). Раскладываем n на простые множители за время  .
.
E. Резервное копирование
В задаче нам дано корневое дерево, на каждом шагу одна из вершин дерева удаляется. При этом, если корень вершины ещё не был удалён, то его значение увеличивается на 1 (изначально все значения равны 1). Если значение какой-то вершины становится равным k, то именно она удаляется на следующем шаге. Требуется максимизировать номер шага на котором будет удалена корневая вершина.
Заметим, что если у корневой вершины менее k - 1 потомка, то можно удалить все вершины дерева, перед тем как трогать вершину номер n. В противном случае, все дети корня разделяются на три множества: те, чьи поддеревья будут удалены полностью, те, у которых корень останется не тронутым, и одно поддерево, после удаления корня которого мы удаляем и саму вершину n. Сделаем обход в глубину нашего дерева и будем поддерживать три значения динамического программирования:
a(v) равняется количеству вершин, которые можно удалить в данном поддереве, если можно удалить вершину v и не обязательно последней. Несложно заметить, что a(v) равняется размеру поддерева.
b(v) равняется количеству вершин, которые можно удалить в данном поддереве, если вершина v должна остаться не тронутой. Равняется a(v) - 1, если у вершины v менее k - 1 сына. В противном случае нужно выбрать каких-то k - 2 потомка, для которых будет использовано значение a(u) и для всех остальных использовать b(u). В качестве таких k - 2 потомков выгодно взять вершины с максимальной разницей a(u) - b(u).
c(v) равняется количеству вершин, которые можно удалить в данном поддереве, если можно удалить вершину v, но она должна быть последней удалённой вершиной поддерева. Величина c(n) и будет являться ответом на задачу. Требуется выбрать какие-то k - 2 потомка, для которых будет использовано значение a(u), одного потомка, для которого мы используем c(u) и для всех остальных к ответу добавится b(u). Переберём, для какого из потомков будет использовано c(u) (то есть кто будет последним удалённым потомком, после чего будет удалена и вершина v). Теперь среди оставшихся требуется взять сумму всех значение b(u) и k - 2 максимальных a(u) - b(u). Для этого достаточно иметь предподсчитанными сумму всех b(u) и список сыновей, упорядоченных по a(u) - b(u). Если вершина x, для которой мы решили взять значение c(x) попадает в вершины с максимальной разностью, то использовать следующую k - 1 вершину (такая обязательно есть, иначе мы просто уничтожаем всё поддерево).
Итоговая сложность решения  .
.
F. Процессоры-лжецы
Воспользуемся тем фактом, что n ≤ 7 и будем вычислять динамику по профилю. Пусть мы заполнили первых i столбцов таблицы, причём на первых i - 1 столбце все процессоры вернули ожидаемый результат. Тогда, для того чтобы продолжить заполнять таблицу нам важно лишь знать, какие из процессоров врут среди последних двух столбцов.
Посчитаем dp(i, m1, m2), где i меняется от 1 до m, а m1 и m2~--- битовые маски от 0 до 2n - 1. Значением динамики будет минимальное количество процессоров-лжецов, которое потребуется, чтобы заполнить первые i столбцов так, чтобы среди первых i - 1 столбца все процессоры вернули ожидаемый результат, а состояние процессоров в последнем и предпоследнем столбце были равны m1 и m2 соответственно. Всего различных состояний O(m·22n). Наконец, для вычисления перехода будет перебирать новую маску m3 и пробовать перейти в состояние dp(i + 1, m2, m3).
Работая с масками с помощью предподсчёта и битовых операций получим результат O(m·23n). Работу программы можно значительно ускорить, если предпосчитать все корректные переходы их каждой пары масок (m1, m2) (то есть запомнить все подходящие к ним маски m3).
Упражнение: придумайте, как получить решение за время O(nm22n).
Всем привет!
Команда проведения чемпионата с радостью сообщает вам, что регистрация на седьмой турнир компании Яндекс по спортивному программированию (а теперь и не только по нему) Яндекс.Алгоритм 2018 уже открыта! Чемпионат является прекрасной возможностью порешать интересные задачи, посоревноваться с любителями спортивного программирования со всего мира, и, возможно, выиграть фирменную футболку. Традиционно, 25 наиболее успешных любителей спортивного программирования будут приглашены принять участия в финальном раунде, который в этом году состоится 19 мая в Санкт-Петербурге.
Если вы уже немного устали решать обычные олимпиадные задачи по программированию, или просто ищете соревновательного разнообразия, то вам, возможно, будет интересно принять участие в двух новых треках: оптимизационном и ML.
Разминочный раунд пройдёт уже в это воскресенье!
UPD: ссылка на разминочный раунд.
UPD2: появился разбор задач!

Задача A. Письма долгого хранения.
В данной задаче требовалось просто просимулировать описанный в условии процесс. Например, можно в любой структуре данных (массив, очередь, дерево) поддерживать множество ещё не обработанных писем и по очереди рассматривать все моменты времени. При рассмотрении момент времени x сначала проверяем, есть ли новое входящее письмо, и, если да, то добавляем его в структуру. Далее проверяем, не наступило ли хотя бы одно из условий, при которых Бомбослава разбирает почту. Для симулирования разбора почты вычисляем число k и последовательно вынимаем k наиболее старых писем из структуры. Даже самая простая реализация этого процесса будет работать за время O(nT).
Упражнение: решите задачу за время O(n).
Задача B. Девчата против автомата.
Для начала заметим, что если Дуся и Люся поделят число n на x и n - x, то они получат в качестве сдачи ровно такой же набор банкнот, как если поделят n на x + 5000 и n - x - 5000. Таким образом, достаточно будет только проверить всем способы разбиения, где x проходит диапазон от a до min(a + 5000, n - a). Для каждого способа вычислим сдачу за время O(1) по следующей формуле: если какая-либо из девушек хочет заплатить величину y, то размер полезной сдачи будет (5000k - y) mod 500, где 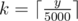 .
.
Упражнение: докажите, что достаточно перебрать значения x в диапазоне от a до min(a + 499, n - a) включительно.
Задача C. Эффективный менеджмент возвращается.
Существует множество различных решений данной задачи, и почти любое из них уложится в ограничение по времени, поскольку в ответе будет использовано не более 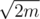 команд (упражнение: доказать это утверждение). Данный разбор будет содержать описание одного из возможных линейных решений.
команд (упражнение: доказать это утверждение). Данный разбор будет содержать описание одного из возможных линейных решений.
Будем добавлять вершины графа по одной. После рассмотрения первых i - 1 вершин (v1, v2, ..., vi - 1) мы будем поддерживать распределение их между ki командами T1, T2, ..., Tki, так что все указанные в условии задачи ограничения выполнены. При добавлении вершины vi найдём любую команду Tj, такую что не существует вершины 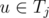 and
and 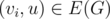 . Полагая
. Полагая 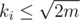 это может быть легко реализовано за время
это может быть легко реализовано за время 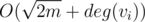 просто с использованием массива булевых пометок и проходом по списку соседей вершины. Если подходящего Tj не существует, то положим ki + 1 = ki + 1, то есть создадим для данной вершины отдельную команду. На самом деле, нам не требуется использовать факт про то, что количество команд есть
просто с использованием массива булевых пометок и проходом по списку соседей вершины. Если подходящего Tj не существует, то положим ki + 1 = ki + 1, то есть создадим для данной вершины отдельную команду. На самом деле, нам не требуется использовать факт про то, что количество команд есть 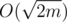 , поскольку вместо обнуления булевого массива мы можем использовать массив специальных пометок. За время O(deg(vi)) расставим пометки всем соединённым с данной вершиной командам, а потом просто пройдём по массиву до тех пор, пока не найдём непомеченную команду. Разумеется, при выполнении этой части будет просмотрено не более deg(vi) + 1 элементов массива и вообще при добавлении вершины будет сделано O(deg(vi)) действий. Таким образом, суммарное время работы есть O(n + m).
, поскольку вместо обнуления булевого массива мы можем использовать массив специальных пометок. За время O(deg(vi)) расставим пометки всем соединённым с данной вершиной командам, а потом просто пройдём по массиву до тех пор, пока не найдём непомеченную команду. Разумеется, при выполнении этой части будет просмотрено не более deg(vi) + 1 элементов массива и вообще при добавлении вершины будет сделано O(deg(vi)) действий. Таким образом, суммарное время работы есть O(n + m).
Задача D. Афера.
Для начала будем несколько иначе воспринимать все ставки. Определим ci = ai + bi, тогда принимая ставку i мы можем считать, что получаем доход bi и должны будем выплатить ci в случае наступления соответствующего исхода. Определим A как некоторое подмножество ставок, 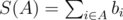 , то есть итоговый доход с данного подмножества без учёта возможных выплат. L(A) положим равному суммарным выплатам, если команда проиграет, то есть
, то есть итоговый доход с данного подмножества без учёта возможных выплат. L(A) положим равному суммарным выплатам, если команда проиграет, то есть  . Аналогично введём величины D(A) и W(A), тогда гарантированный доход Остапа с подмножества A равен S(A) - max(L(A), D(A), W(A)).
. Аналогично введём величины D(A) и W(A), тогда гарантированный доход Остапа с подмножества A равен S(A) - max(L(A), D(A), W(A)).
В данном виде пока ещё непонятно как решать задачу, поскольку требуется с одной стороны увеличивать S(A), и минимизировать максимум с другой стороны. Зафиксируем max(L(A), D(A), W(A)) = k, тогда задача звучит как: какова максимальная стоимость по bi подмножества ставок с исходом "поражение" ("ничья", "победа"), которое можно принять так чтобы сумма их ci не превосходила k. Соответствующие значения 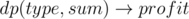 можно независимо посчитать для каждого исхода с помощью динамического программирования решающего задачу о рюкзаке. Сложность такого решения будет O(nL), где
можно независимо посчитать для каждого исхода с помощью динамического программирования решающего задачу о рюкзаке. Сложность такого решения будет O(nL), где  .
.
Задача E. Случайная величина моды.
Сперва рассмотрим решение задачи за время O(n2) с помощью динамического программирования. Положим dpleft(i, j) равным оптимальному ожидаемому времени в торговом центре, если Глеб уже обошёл все магазины с i по j включительно и сейчас стоит рядом с магазином i. Аналогично положим dpright(i, j) равным оптимальному ответу если Глеб обошёл магазины с i по j и стоит около магазина j.
Мы не будем приводить всех формул в данном разборе, но, например, dpleft(i, j) может быть вычислено как минимум из двух возможных переходов (в i - 1 или j + 1) следующим образом:
,
Для ускорения решения задачи заметим, что если не существует магазинов с pi = 0, то мы посетим большое количество магазинов с очень маленькой вероятностью, поскольку уже вероятность в один процент, то есть 0.01 является достаточно большой. Вероятность посетить k магазинов с pi > 0 и всё ещё не найти подходящий плащ составляет 0.99k, что для k = 5000 составит порядка 1.5·10 - 22. используя что ti ≤ 1000 и n ≤ 300 000 получаем, что на посещение всего торгового центра потребуется не более 109 секунд, то есть уже при k = 5000 влияние на ответ составит не более 10 - 12. На самом деле, учитывая, что нам разрешается допустить относительную ошибку 10 - 6 достаточно будет k = 3000.
Теперь найдём не более k магазинов с pi > 0 и i < x и не более k магазинов с pi > 0 и i > x (то есть слева и справа от стартового). Далее сожмём магазины с pi = 0 и применим квадратичную динамику. Итоговое время работы составит O(n + k2).
Задача F. Семь раз отмерь, один раз раздели.
Каждой вершине требуется назначить неотрицательное целое число xv равное номеру итерации описанного в условии процесса, на которой данная вершина будет удалена. По причинам, которые станут понятны читателю в дальнейшем, мы будем считать, что xv = 0 означает удаление на самой последней итерации, то есть б**о**льшие значение x будут соответствовать более ранним итерациям процесса. Можно показать, что фиксированные значения xv корректно описывают процесс, если и только если для любых двух вершин u и v, таких что xu = xv максимальное значение xw по всем w лежащим на пути от u до v больше xu. Другими словами, наличие на любом пути между двумя одинаковыми значениями другого значения, которое больше их обоих, означает, что любые две вершины, удаляемые на одном шаге, будут к этому моменту находиться в разных компонентах.
Выберем любую вершину в качестве корня дерева. Обозначим через C(v) множество непосредственных детей вершины v, а через S(v)~--- поддерево вершины v. Теперь, если в поддереве v уже зафиксирована некоторая корректная расстановка значений x, то нас интересуют только те xu, 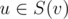 , которые ещё никем не перекрыты, то есть на пути от u до вершины корня поддерева (вершины v) нет значения больше xu. Через d(v, mask) обозначим булево значение, возможно ли так расставить x в поддереве вершины v, чтобы незакрытыми оставались только значения из множества mask. Поскольку благодаря центроидной декомпозиции мы знаем, что величина ответа не превзойдёт
, которые ещё никем не перекрыты, то есть на пути от u до вершины корня поддерева (вершины v) нет значения больше xu. Через d(v, mask) обозначим булево значение, возможно ли так расставить x в поддереве вершины v, чтобы незакрытыми оставались только значения из множества mask. Поскольку благодаря центроидной декомпозиции мы знаем, что величина ответа не превзойдёт 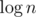 , то интересных значений mask не более
, то интересных значений mask не более 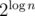 , то есть O(n). Значения d(v, mask) можно вычислить если известны d(u, mask) для всех
, то есть O(n). Значения d(v, mask) можно вычислить если известны d(u, mask) для всех 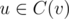 за время O(n3) используя следующие соображения (обозначим через u1, u2, ... детей из C(v), а через m1, m2, ... рассматриваемые в них значения динамики):
за время O(n3) используя следующие соображения (обозначим через u1, u2, ... детей из C(v), а через m1, m2, ... рассматриваемые в них значения динамики):
- Значение xv должно быть больше любого i, которое встречается более чем в одной маске mi.
- Значение xv должно быть равно какому-нибудь i, которое не встречается ни в одной mi.
- Если мы положим xv = i, то все j < i будут равны 0 в m.
Заметим, что согласно описанному выше процессу если маска m1 является подмаской m2, то она всегда лучше влияет на ответ, чем m2. Теперь мы утверждаем, что если рассмотреть минимальное m, такое что d(v, m) = true, то для любой m1 > m найдётся m2 подмаска m1, такая что d(v, m2) = true. В самом деле, рассмотрим первый (старший) бит i, в котором m и m1 отличаются. Поскольку m1 больше m, то в этой позиции у неё будет записано 1, а у m будет записан 0. Если после этого в m вообще нет 1, то она сама является подмаской m1, в противном случае это означает, что xv < i. Выставим xv = i и получим подмаску m1.
Доказанное выше означает, что достаточно только рассмотреть лексикографически минимальную маску, которую можно получить в каждом из поддеревьев S(v). Для этого будем объединять ответы по всем 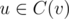 используя вышеописанную процедуру. Такое решение может быть легко реализовано за время
используя вышеописанную процедуру. Такое решение может быть легко реализовано за время  или даже O(n) при эффективном использовании битовых операций.
или даже O(n) при эффективном использовании битовых операций.
Всем привет!
Завтра, в 10:00 мск состоится Раунд 1 соревнования Яндекс.Алгоритм, автором задач которого являюсь я. Хочу сказать спасибо Zlobober за помощь в подготовке раунда и за всю ту работу, которую он делает чтобы данное соревнование было интересным и качественным, а также MikeMirzayanov за замечательную платформу polygon, значительно облегчающую процесс разработки задач, а также всем, кто прорешивал раунд и давал ценные комментарии. Разумеется, мы приложили максимум усилий, чтобы сделать задачи разнообразными как по сложности, так и по тематике.
До встречи на соревновании!
UPD Спасибо всем, кто принял участие, надеюсь каждый нашёл для себя хотя бы одну интересную задачу. Мы приносим свои извинения за ситуацию с задачей F, мы честно искали все задачи в интернете и спрашивали у тестеров, не видели ли они аналогичных задач, но это не помогло. Опубликован разбор задач (пока только на английском).
I've already expressed everything in this comment, however, I've decided to additionally create this post to raise the attention to what I consider to be a very serious and frustrating issue.
Всем привет!
Завтрашний раунд пройдёт на наборе задач Московской олимпиады школьников по программированию для 6-9 классов. Пусть вас не смущает возраст участников, московская методическая комиссия постаралась отобрать для олимпиады разнообразные и интересные задачи. Непосредственной разработкой задач занимались feldsherov, ch_egor, halin.george, ipavlov и GlebsHP.
Надеемся увидеть вас завтра в таблице результатов!
P.S. Будет использована стандартная разбалловка.
UPD Поздравляем победителей раунда!
UPD2 А вот и разбор задач.
Всем привет!
Если вдруг вы очень хотели написать короткий тур заочного этапа, и расстраивались, что он доступен только для официальных участников с определённым количеством баллов, то спешим вас порадовать. Жюри приняло решение провести внеконкурсную трансляцию для всех желающих. Ссылка на вход в соревнование. Контест можно стартовать до 23:59:59 23 января (понедельник).
Дорогие друзья!
Это был великолепный год, и я получил огромное удовольствие, работая координатором Codeforces. За этот год я научился очень многому, пообщался с множеством интересных людей и проникся тем, как важно, чтобы твою работу ценили тысячи людей. Спасибо каждому из вас за это! Я уверен, вас ждут клёвые раунды и занимательные задачи (и конкурсы интересные), ведь я передаю эту должность Николаю KAN Калинину!
Посмотрите моё новогоднее обращение (русский язык, английские субтитры):
P.S. За помощь в подготовке видео отдельное спасибо Максиму Zlobober Ахмедову и Олегу mingaleg Мингалёву.
Finally, the analysis is here! Feel free to ask in comments for any unclear part.
Problems ideas and development:
Cards: MikeMirzayanov, fcspartakm
Cells Not Under Attack: GlebsHP, fcspartakm
They Are Everywhere: MikeMirzayanov, fcspartakm
As Fast As Possible: GlebsHP, fcspartakm
Connecting Universities: GlebsHP, fcspartakm, danilka.pro
Break Up: GlebsHP, MikeMirzayanov, kuviman
Huffman Coding on Segment: GlebsHP, Endagorion
Cool Slogans: GlebsHP
Всем привет!
Сегодня состоится второй и последний регулярный рейтинговый раунд, составленный с использованием задач VK Cup 2016 Final Round. Разумеется, как и в предыдущий раз, был дополнительно подготовлен набор простых задач, чтобы контест был интересен всем участникам.
В прошлый раз в комментариях указали, что я забыл поблагодарить MikeMirzayanov за великолепные платформы Codeforces и Polygon. Исправляюсь, Миша, реально норм :)
Разбалловка будет опубликована ближе к началу раунда. Желаем удачи и красивых решений!
UPD1. Разбалловка div2: 500-750-1000-1500-2000-2500. Разбалловка div1: 500-1000-1500-2250-3000.
UPD2. Соревнование завершено, поздравляем победителей!
Div1: 1. ainta 2. W4yneb0t 3. Petr 4. muratt 5. kcm1700 6. Vercingetorix 7. Tinsane 8. Reyna 9. aid 10. zemen
Div2: 1. MinamiKotori 2. Ancient_mage 3. WhatTheFua 4. Yanba 5. macieck9 6. OMRailgun 7. radoslav11 8. zhsh 9. skywalkert 10. abgnwl
Разбор задач будет появляться здесь по мере готовности.
Дорогие друзья!
Мы рады представить вам Codeforces Round #363, который пройдёт с частичным использованием задач прошедшего в начале июля в Санкт-Петербурге VK Cup 2016 Final Round. Вторая часть задач чемпионата будет использована при проведении Codeforces Round #364. Разумеется, мы дополнили набор задач до полноценного раунда Codeforces, чтобы каждый мог найти задачу подходящей сложности, которая ему будет интересна.
Не желая изменять доброй традиции, мы опубликуем разбаловку непосредственно перед началом соревнования.
Желаем вам удачи и удовольствия от решения задач!
UPD1. Стоимости задач будут стандартными 500-1000-1500-2000-2500-3000 для обоих дивизионов (да, в обоих дивизионах будет предложено для решения шесть задач).
UPD2. Задачи были подготовлены для вас MikeMirzayanov, Errichto, fcspartakm, qwerty787788 и Radewoosh.
UPD3. Системное тестирование завершено, поздравляем победителей!
Div. 1:
Div. 2:
UPD4. Разбор уже здесь, планируется в скором времени перевести его на русский язык.

20 марта в 15:00 начнётся второй квалификационный раунд чемпионата VK Cup 2016!
Правила этого раунда будут совпадать с правилами Квалификации 1. К участию приглашаются команды, не участвовавшие в первой квалификации или набравшие в ней менее 4800 баллов. Те, кто успешно справился с первой квалификацией, могут принять участие вне конкурса, при этом их результаты никак не будут влиять на проход остальных команд. Разумеется, от команд, участвующих вне конкурса, также требуется соблюдение всех правил Чемпионата.
Во время Квалификации 1 нас приятно удивил рост уровня подготовки участников — тот факт, что для прохода необходимо было сдать все четыре задачи, стал для нас большой неожиданностью. Разумеется, мы учли это при подготовке Квалификации 2, посмотрим, как вы справитесь на этот раз :)
Раунд продлится 24 часа, такая продолжительность выбрана для того, чтобы все нашли себе удобное время для участия. Квалификационный раунд, как и все предстоящие раунды, требует отдельной регистрации, она будет открыта на протяжении всего раунда.
При регистрации на раунд состав вашей команды фиксируется и не подлежит дальнейшей модификации. Вы не сможете в будущем добавить или удалить члена команды. Пожалуйста, перед регистрацией убедитесь, что у вас нет желания изменить состав. Состав команды не сможет быть изменен, даже если вы отмените регистрацию на квалификационный раунд.
В Раунд 1 пройдут все команды, которые наберут положительное количество баллов, не меньше количества баллов у команды на 500-м месте.
Во время квалификации задачи тестируются системой только на претестах, а системное тестирование состоится после окончания раунда. Обратите внимание, что претесты не покрывают все возможные случаи входных данных, поэтому тщательно тестируйте свои программы! Взломов, падения стоимости задач во время квалификации не будет. Время сдачи задач не будет учитываться, однако будут учитываться штрафные попытки.
Категорически запрещается публиковать где-либо условия задач/решения/какие-либо мысли и соображения о них до окончания раунда. Запрещено обсуждать задачи с кем-либо, кроме вашего сокомандника. Будьте честны, пусть в Раунд 1 пройдут сильнейшие!
После окончания раунд станет доступен всем для дорешивания, а его задачи попадут в архив, в том числе и на английском языке.
Это был бы самый обычный разбор, если бы не новая фича — спойлеры. Заценить как это круто и удобно можно уже прямо в этом посте, к каждой задаче под спойлером прикладывается код решения. Скажем спасибо kuviman :)
Текст разбора: MikeMirzayanov, fcspartakm и GlebsHP.
637A - Голосование за фотографии
Автор идеи: MikeMirzayanov. Разработка: fcspartakm.
Для решения данной задачи достаточно было проитерироваться по поставленным лайкам в хронологическом порядке и в отдельном массиве поддерживать количество лайков, которые уже были поставлены фотографиям (например, в cnt[i] будет храниться количество лайков, поставленных i-й фотографии). Для нахождения ответа достаточно на каждой итерации обновлять имеющийся максимум лайков текущим значением cnt[i], и если cnt[i] > maxCnt обновлять ответ, где maxCnt — это текущее максимальное количество лайков.
Асимптотика такого решения — O(n), где n — количество поставленных лайков.
Основная часть решения:
int n;
int a[N];
int cnt[M];
int main() {
scanf("%d", &n);
int maxCnt = 0, ans;
for (int i = 0; i < n; i++) {
scanf("%d", &a[i]);
cnt[a[i]]++;
if (cnt[a[i]] > maxCnt) {
ans = a[i];
maxCnt = cnt[a[i]];
}
}
printf("%d", ans);
}
637B - Порядок чатов
Автор идеи: GlebsHP. Разработка: fcspartakm.
Для решения данной задачи нужно проитерироваться в обратном порядке по адресатам сообщений, начиная с последнего, так как верно то, что чем позднее Поликарп отправит сообщение какому-то собеседнику, тем выше этот собеседник будет в списке чатов. На каждой итерации нужно проверять, что текущий собеседник еще не был добавлен в список чатов (то есть Поликарп еще не писал ему сообщение). Это можно сделать с помощью структуры данных set. Таким образом, если текущего собеседника еще нет в списке чатов, нужно добавить имя этого собеседника в конец ответного списка чатов и добавить имя этого собеседника в set.
Асимптотика такого решения — O(n·log(n)), где n — количество сообщений, отправленных Поликарпом.
Основная часть решения:
int n;
string a[N];
set<string>names;
int main () {
cin >> n;
for (int i = 0; i < n; i++) {
cin >> a[i];
}
for (int i = n - 1; i >= 0; i--) {
if(names.count(a[i]))
continue;
names.insert(a[i]);
cout << a[i] << endl;
}
}
637C - Промокоды с ошибками
Автор идеи: GlebsHP. Разработка: GlebsHP.
Для начала научимся решать задачу проверки фиксированного значения k. Правда ли, что если мы в каждом промокоде совершим не более чем k ошибок, ты мы сможем однозначно идентифицировать исходных промокод? Иначе говоря, верно ли, что для любой последовательности из шести цифр, существует не более одного промокода отличающегося от данной последовательности в k или менее позициях.
Для каждого промокода можно построить множество последовательностей отличающихся от него не более чем в k позициях, то есть шар радиуса k в данной метрике. Так, для промокода 123456 подойдут последовательности ?23456, 1?3456, 12?456, 123?56, 1234?6 и 12345? (вопросик заменяется на любую цифру). Очевидно, что некоторое k подходит, если никакие два шара радиуса k не пересекаются. Этого уже достаточно для решения задачи, просто честно перебрать значения k и проверить наличие пересечения шаров. Единственная тонкость — процесс необходимо остановить как только найдётся любая последовательность принадлежащая двум шарам.
Благодаря условию n ≤ 1000 задачу можно было решить и гораздо проще. Заметим, что два шара радиуса k пересекаются если расстояние между их центрами не превосходит 2·k. Таким образом достаточно найти пару прокодов с минимальным расстоянием между ними и выбрать максимальное подходящее k. Не забываем про случай n = 1.
Основная часть решения:
int calc_dist(const string& s1, const string& s2) {
int d = 0;
for (int i = 0; i < (int) s1.size(); i++)
d += (s1[i] != s2[i]);
return d;
}
int main() {
int n;
cin >> n;
vector <string> code(n);
for (int i = 0; i < n; i++)
cin >> code[i];
int ans = 12;
for (int i = 0; i < n; i++)
for (int j = i + 1; j < n; j++)
ans = min(ans, calc_dist(code[i], code[j]) - 1);
cout << ans / 2 << endl;
return 0;
}
637D - Бег с препятствиями
Автор идеи: MikeMirzayanov. Разработка: fcspartakm.
В самом начале отсортируем все координаты препятствий по возрастанию. Затем воспользуемся следующим фактом: если спортсмен может преодолеть препятствие номер x и успевает разбежаться перед прыжком до препятствия номер x + 1 (то есть s ≤ a[x + 1] - a[x] - 2, где s — длина разбега перед прыжком), ему выгодно разбежаться и начать новый прыжок в точке a[x + 1] - 1.
Таким образом, для решения задачи достаточно проитерироваться по препятствиям слева направо. Пусть спортсмен преодолеть препятствие с номером i. Тогда нужно найти первое такое препятствие с номером j (правее i), что спортсмен успеет разбежаться для прыжка после препятствия j - 1 и до препятствия j. В таком случае спортсмену необходимо выполнить прыжок из точки a[i + 1] - 1 в точку a[j - 1] + 1. Если расстояние между этими точками больше чем d, значит спортсмен не сможет добраться до финиша. В противном случае нужно выполнить такой прыжок и продолжить работу программы. После преодоления всех препятствий нужно проверить нужно ли спортсмену бежать до финишной точки, или он уже находится в ней.
Асимптотика такого решения —  , где n — количество препятствий.
, где n — количество препятствий.
Основная часть решения:
int a[N];
int n, m, s, d;
vector<pair<string, int> > ans;
int main () {
cin >> n >> m >> s >> d;
for(int i = 0; i < n; i++) {
cin >> a[i];
}
sort(a, a + n);
int curPos = 0;
for (int i = 0; i < n; ) {
int prev = i;
if(a[i] - curPos - 1 >= s) {
i++;
while(i < n && a[i] - a[i - 1] - 2 < s)
i++;
int jumpDist = a[i - 1] + 1 - (a[prev] - 1);
if (jumpDist > d) {
cout << "IMPOSSIBLE" << endl;
return 0;
}
ans.push_back(make_pair("RUN", a[prev] - curPos - 1));
ans.push_back(make_pair("JUMP", jumpDist));
curPos = a[i - 1] + 1;
} else {
cout << "IMPOSSIBLE" << endl;
return 0;
}
}
if(curPos != m)
ans.push_back(make_pair("RUN", m - curPos));
for(int i = 0; i < (int)ans.size(); i++) {
cout << ans[i].first << ' ' << ans[i].second << endl;
}
}
Добрый день, уважаемое сообщество!
Завтра мы проведём Codeforces Round #342. Раунд пройдёт на задачах Московской олимпиады для 6-9 классов, но не надо думать что из-за этого задачи будут простыми. Гарантирую, что все (в том числе участники из первого дивизиона) найдут для себя что-нибудь интересное. Задачи были отобраны для вас жюри московских олимпиад: Zlobober, meshanya, romanandreev, Еленой Владимировной Андреевой и мной; подготовили задачи члены нашего научного комитета: wilwell, Sender, iskhakovt, thefacetakt и feldsherov.
Разбалловка будет достаточно необычной: 750-750-1000-2000-3000.
UPD Системное тестирование завершено, поздравляем победителей:
Сложность задач оказалась несколько выше, чем требовалось, возможно стоило подготовить раунд для Div. 1 тоже. В любом случае, спасибо всем за участие, я надеюсь вам понравилось и вы узнали что-нибудь новое!
Спасибо romanandreev за отличный разбор задач.
Добрый день, дорогие пользователи Codeforces!
2 ноября начался заочный этап X Открытой олимпиады школьников по программированию. В контест добавлен первый пакет из пяти задач, остальные задачи будут добавлены позднее. Те из вас, кто знает что такое Открытая олимпиада (она же "заочка") и её правила, могут не читать дальше и сразу переходить на сайт олимпиады :) Первый пакет задач подготовили для вас: Zlobober, romanandreev, snarknews и GlebsHP.
Те, кто раньше в данной олимпиаде не участвовал, могут так же пойти на сайт и прочитать полную информацию там, а в этом посте будут обозначены лишь основные моменты. Олимпиада состоит из двух этапов: заочного и очного. Заочный этап проходит со 2 ноября по 18 января, и традиционно состоит из 10-15 задач различной сложности, тематики и формата. Мы подбираем задачи таким образом, чтобы они были интересны как совсем новичкам, так и "зубрам" олимпиадной информатики. Лучшие n участников (n приблизительно равно 400) будут приглашены на очный этап олимпиады.
Очный этап пройдёт в Москве, ориентировочные даты проведения — 7-8 марта. Площадка проведения — учебный центр нашего генерального спонсора 1С на м. Тимирязевская. Также, благодаря нашему спонсору, участникам оплачивается проживание в гостинице на время проведения олимпиады. Очный этап состоит из двух туров, уровень участников немного превосходит уровень Всероссийской олимпиады по информатике за счёт приезда сильных школьников из ближнего зарубежья. Возможно это прозвучит слишком пафосно, но на наш вкус качество задач олимпиады в последние годы превосходит Всероссийскую олимпиаду и сравнимо с IOI. Олимпиада имеет первый уровень и даёт соответствующие льготы при поступлении.
Призеры заочного этапа олимпиады никаких льгот не имеют — поступить, не выходя из дома, всё-таки не получится.
Для тех, кто не является школьником и хочет просто порешать задачи, доступно внеконкурсное участие.
Жюри олимпиады призывает всех участников действовать честно, не обсуждать друг с другом решения задач и не делиться написанным кодом. Особенно хотим отметить, что любое обсуждение задач запрещено, в частности, и в комментариях на Codeforces (в том числе, и к этому посту). Все интересующие вас вопросы по задачам вы можете и должны задавать через тестирующую систему. К сожалению, каждый год некоторые участники заочного этапа не допускаются к участию в очном этапе из-за выявления случаев списывания с их участием.
Любые оставшиеся вопросы смело задавайте в комментариях.
UPD: в контест добавлены четыре новые задачи: F, G, H и I. Для вас их подготовили: thefacetakt, Sender, haku и ipavlov.
UPD2: в контест добавлены последние три задачи: J, K и L. За подготовку задач мы благодарим: romanandreev, Vaness и mingaleg.
UPD3: на сайте олимпиады доступны предварительные результаты и архив олимпиады. Рады сообщить, что Zlobober подготовил для вас разбор задач заочного этапа.
Мне нравится идея Endagorion дополнять разбор задач небольшими упражнениями, связанными с подготовкой задачи, её обобщением или наличием более эффективного решения. Попробуем и мы предложить читателю подобные вопросы по некоторым задачам.
Div. 2A (Поединок волшебников)
Автор идеи: Роман Гусарев, разработка: timgaripov.
Найдем координату первого столкновения импульсов. Они сближаются со скоростью p + q, а значит первое столкновение произойдёт через 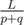 секунд. Следовательно, координата первого столкновения может быть вычислена как
секунд. Следовательно, координата первого столкновения может быть вычислена как 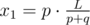 .
.
Заметим теперь, что расстояние проходимое импульсами на обратном пути до волшебников равно расстоянию проходимому ими от волшебников до места первой встречи. Это значит, что импульсы вернутся к волшебникам одновременно, и ситуация станет идентична изначальной. Таким образом, вторая встреча (и все последующие) произойдёт в той же точке, что и первая.
Пример решения: 13836780.
Div. 2B (Ребрендинг)
Автор идеи: glebushka98, разработка: thefacetakt.
Тривиальное решение: будем эмулировать работу дизайнеров, а именно каждый раз ходить и честно перекрашвать все xi в yi и наоборот. Работает за 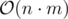 , получает TL.
, получает TL.
Попробуем улучшить этот результат.
Заметим, что одинаковые буквы переходят в одинаковые. Это означает, что позиция буквы никак не влияет на результат, и достаточно помнить для каждого возможного значения символа, во что он перейдёт. Пусть p(i, c) — символ, который будет стоять вместо всех вхождений c после обработки i дизайнеров. Тогда:
- p(0, c) = c
- Если p(i - 1, c) = xi, то p(i, c) = yi
- Аналогично, если p(i - 1, c) = yi, то p(i, c) = xi
Данное решение работает уже за O(|Σ|·m + n) и проходит все тесты.
Упражнение: доведите решение данной задачи до сложности O(Σ + n + m).
Примеры решения: 13837577 за O(|Σ|·m + n) и 13839154 за O(|Σ| + n + m).
Div. 2C\Div. 1A (Медианное сглаживание)
Автор идеи и разработчик: Sender.
Назовём статичными точками позиции, которые не могут измениться, сколько бы раз мы не применяли к последовательности алгоритм медианного сглаживания. Оба конца являются статичными точками по определению. Также, легко заметить, что если рядом стоят два одинаковых символа, то обе эти позиции так же являются статичными точками.
Исследуем влияние статичных точек на соседние элементы. Пусть ai - 1 = ai, то есть элемемнты i - 1 и i являются статичными точками. Пусть также ai + 1 статичной точкой пока не является, следовательно ai + 1 ≠ ai и ai + 1 ≠ ai + 2. Из предыдущего предложения и того, что возможны только 0 и 1 делаем вывод, что ai = ai + 2 и после одного применения алгоритма медианного сглаживания будет выполнено ai = ai + 1. То есть любая статичная точка за один шаг превращает все соседние элементы в статичные точки. Таким образом, любая последовательность в итоге стабилизируется.
Остаётся только вычислить скорость стабилизации и результирующие значения. Заметим, что если между двумя статичными точками i и j нет других статичных точек, то это означает чередование всех символов между позициями i и j. Несложно проверить, что в чередующейся последовательности новые статичные точки не образуются, следовательно последовательность будет оставаться чередующейся пока до неё не дойдёт влияние одной из соседних статичных точек.
Итоговое решение: выделим все статичные точки в изначальной последовательности и найдём max(min(|i - sj|)), где sj — множество индексов позиций статичных точек. Сложность решения O(n).
Упражнение 1: взломайте решение честно моделирующее применение алгоритма медианного сглаживания до стабилизации процесса.
Упражнение 2: придумайте как ускорить квадратичное решение с помощью битового сжатия (и всё равно получить TL).
Примеры решений: 13838940 и 13838480.
Div. 2D\Div. 1B (Чип и Дейл спешат на помощь)
Автор идеи и разработчик: StopKran.
Заметим, что если собственная скорость дирижабля задана вектором (ax, ay), а скорость ветра вектором (bx, by), то реальный вектор движения дирижабля определяется как (ax + bx, ay + by).
Одним из ключевых моментов в решении задачи является понимание монотонности функции ответа по времени. Если дирижабль может достичь цели за  секунд, то он сможет достичь её и за
секунд, то он сможет достичь её и за 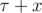 секунд, для любого x ≥ 0. Это очевидно вытекает из условия, что максимально возможная собственная скорость дирижабля строго превосходит скорость ветра в любой момент времени.
секунд, для любого x ≥ 0. Это очевидно вытекает из условия, что максимально возможная собственная скорость дирижабля строго превосходит скорость ветра в любой момент времени.
Поскольку функция ответа монотонна, воспользуемся методом бинарного поиска по ответу, а именно, научимся проверять для фиксированного параметра  , возможно ли добраться от точки (x1, y1) до точки (x2, y2) за время
, возможно ли добраться от точки (x1, y1) до точки (x2, y2) за время  . Будем учитывать перемещение под действием ветра и собственное перемещение отдельно. Найдём сперва смещение дирижабля вызванное ветром:
. Будем учитывать перемещение под действием ветра и собственное перемещение отдельно. Найдём сперва смещение дирижабля вызванное ветром:
- (xn, yn) =
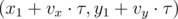 , если
, если 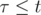 ;
; - (xn, yn) =
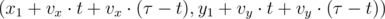 , если
, если 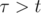 .
.
Остаётся только проверить, что используя только лишь собственную скорость можно добраться за время  из точки (xn, yn) в точку (x2, y2).
из точки (xn, yn) в точку (x2, y2).
Итоговая сложность: 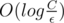 , где C — максимальная координата, а ε — требуемая точность.
, где C — максимальная координата, а ε — требуемая точность.
Упражнение 1: подумайте как решить задачу, в случае когда не гарантируется, что дирижабль всегда быстрее ветра.
Упражнение 2: можете ли вы решить задачу за время O(1)?
Примеры решений: 13838659 и 13842505.
Div. 2E\Div. 1C (Три государства)
Автор идеи и разработчик: haku.
Утверждение. Пусть в неориентированном невзвешенном связном графе выделенны три различные вершины u, v, w. Одна из минимальных сетей, связывающих выделенные вершины, выглядит как некоторая вершина графа c, возможно совпадающая с одной из выделенных, из которой исходят кратчайшие пути к каждой из выделенных вершин, причём эти пути являются вершинно-непересекающимися.
Доказательство. Одним из оптимальных связывающих подграфов обязательно является дерево. Действительно, в противном случае на любом цикле найдётся ребро, которое можно выкинуть, и это не ухудшит ответ, поскольку он не зависит от количества используемых рёбер. Листьями дерева могу являться только вершины u, v и w, иначе ответ можно было бы улучшить, просто выкинув такой листь. Дерево, у которого не более чем три листа, имеет не более одной вершины степени больше двух, которая и будет вершиной c из утверждения выше. Разумеется, любой путь от c до листа имеет смысл заменить на кратчайший. Отдельно возможен вырожденный случай, что дерево ответа — это бамбук, но в таком случае вершиной c является одна из трёх выделенных вершин (не лист).
Теперь имеем следующий метод для нахождения длины кратчайшей связывающей сети: перебрать все вершины, включая выделенные, и из сумм кратчайших расстояний от данной вершины до выделенных выбрать минимальную. Ясно, что таким образом мы переберём длины различных связывающих сетей, среди которых будет и длина кратчайшей, и поэтому минимум будет ответом.
Для сведения исходной задачи к задаче поиска минимальной связывающей сети, можно представить карту в виде графа, где вершинам соответствуют клетки, принадлежащие государствам или допускающие постройку дороги, а ребро между двумя вершинами ставится, если они являются соседними в таблице. Все вершины, соответствующие одному государству, необходимо сжать в одну. Несложно заметить, что исходная задача таким образом свелась к вышеописанной.
Примеры решений: 13843265 — описанное решение реализовано через бфс на 0-1 графе, 13840329 — здесь логика решения несколько иная, разбираются два принципиально разных случая.
Div. 1D (Сверхсекретное задание)
Автор идеи и разработчик: glebushka98.
Если 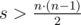 , то ответом является сумма k минимальных элементов.
, то ответом является сумма k минимальных элементов.
Пусть i1 < i2 < ... < ik — индексы элементов, которые войдут в итоге в ответ. Заметим, что относительный порядок выбранных элементов менять не имеет смысла, а значит, мы можем однозначно сказать, какой из выбранных элементов займёт какую позицию в ответе. T — минимальное количество операций, за которое их можно поставить на k первых мест. 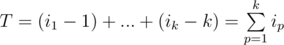 —
— 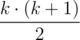 .
.
T ≤ S 
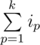 ≤
≤ 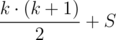 .
. 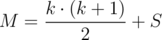 .
.
Посчитаем динамику d[i][j][p] — минимально возможная сумма, если среди первых i элементов выбрать j с суммой индексов не больше p. В целях оптимизации использования памяти будем хранить каждый раз только два верхних уровня динамики.
Итоговая сложность решения: O(n4) по времени и O(n3) по памяти.
Примеры решений: 13845513 и 13845571.
Div. 1E (День рождения)
Автор идеи: meshanya, разработчик: romanandreev.
Задача естественно разбивается на две подзадачи: быстрое построение графа вложенности и нахождение максимального независимого множества в этом графе. Заметим сразу, что если строка s2 является подстрокой строки s1, а строка s3 является подстрокой строки s2, то s3 очевидно является подстрокой строки s1. Таким образом, граф вложений зададаёт частично упорядоченное множество.
Для быстрого построения графа воспользуемся алгоритмом Ахо-Корасик. С помощью данной структуры мы построим все существенные рёбра графа, то есть такие рёбра  , что не найдётся w, такого что
, что не найдётся w, такого что  и
и  . Одним из возможных способов является:
. Одним из возможных способов является:
- Построить структуру Ахо-Корасик;
- Для каждой вершины найти и запомнить ближайшую терминальную в суффиксном пути;
- Ещё раз скормить каждую строку автомату Ахо-Корасик, при этом каждый раз после добавления очередного символа требуется проводить ребро в ближайшую терминальную вершину в суффиксном пути;
- Кроме существенных рёбер, данный алгоритм возможно добавит ещё какие-то корректные рёбра, но это никак не влияет на результат работы следующего шага;
- Транзитивно замкнуть построенный граф.
Для решение второй части данной задачи требует применить теорему Дилворта. Восстановление ответа следует из конструктивного доказательства теоремы.
Получаем O(L + n3) на построение графа + O(n3) на нахождение максимальной антицепи, итоговая сложность решения: O(L + n3), где L — суммарная длина всех строк.
Поздравляем ikatanic — единственного человека сдавшего эту задачу во время тура. Для дальнейшего уточнения решения предлагается посмотреть 13851141.
Упражнение: научитесь решать задачу с сохранением асимптотики, при условии что требуется найти множество строк максимальное не по размеру, а по суммарной длине.
Здравствуйте, уважаемые участники сообщества Codeforces!
Начиная с Codeforces Round #327, я буду координировать подготовку регулярных раундов и прочих контестов, которые проводятся на платформе Codeforces. Обещаю приложить максимум усилий, чтобы улучшить качество подготовки контестов, хотя это и будет проблематично сделать — Zlobober установил высокую планку. Давайте ещё раз поблагодарим Максима за хорошо проделанную работу!
Завтрашний раунд проводится на задачах Московcкой городской командной олимпиады по программированию среди школьников. Пусть вас не смущает, что это школьное соревнование, — среди участников есть золотой призёр IOI 2015 и несколько кандидатов в сборную России этого года, поэтому мы постарались сделать все задачи интересными, а некоторые ещё и сложными. Уверен, что каждому из вас должна понравиться хотя бы одна задача предстоящего раунда.
Задачи были подготовлены коллективом московских авторов в составе (список пополняется): Zlobober, romanandreev, meshanya, wilwell, glebushka98, timgaripov, thefacetakt, haku, LHiC, Timus, Sender, sankear, iskhakovt, andrewgark, ipavlov, StopKran, AleX. Руководство подготовкой осуществляли ваш покорный слуга GlebsHP и председатель жюри олимпиады Андреева Елена Владимировна.
Отдельно благодарим Delinur за перевод условий на английский язык и stella_marine за вычитку.
В каждом дивизионе будет предложено для решения пять задач, разбаловка будет опубликована позднее (не будем нарушать эту традицию).
UPD. Время раунда. Обратите внимание, что во многих странах мира этой ночью переводят часы, а в России не переводят — не пропустите случайно раунд :)
UPD2. Обратите внимание, разбаловка как бы намекает, что надо прочитать все задачи! Div1.: 750-1000-1250-1750-2500 Div2.: 500-1000-1750-2000-2250
UPD3. Результаты раунда и разбор будут опубликованы позднее, когда завершится официальное соревнование.
UPD4. Системное тестирование завершено, доступны окончательные результаты, открыто дорешивание задач. Поздравляем победителей в первом дивизионе:
UPD5. Появился разбор.
| Название |
|---|










