Сначала расположим задачи по сложности, как предполагалось авторами: A, D, B, C, E. Теперь разберем задачи по порядку следованию в соревновании.
Эта задача носила технический характер. Сначала нужно было удалить все вхождения слова WUB в начале и в конце исходной строки. А затем распарсить оставшуюся строку, разделяя токены словом WUB. Пустые токены нужно было пропустить. Ограничения были небольшие, реализовать это можно было как угодно.
В этой задаче можно было написать поиск в ширину. В качестве состояния можно взять следующую четверку: количество оставшихся стопок, а также три строки, которые обозначают три крайние правые карты на трех крайний стопках. Соответственно мы имеем два перехода в общем случае, когда перекладываем последнюю карту на 1, либо на 3 влево. Если количество стопок в какой-то момент окажется равным 0 выводим YES, иначе NO. Состояний O(N4), переходов 2, итого временная сложность решения O(N4).
208C - Контрольный пункт полиции
В данной задаче для каждой вершины отдельно посчитаем искомую величину и найдем среди них максимальную. Для этого для каждой вершины v посчитаем две величины: cnt1[v] и cnt2[v] — количество кратчайших путей из вершины v в n-ую вершину и 1-ую вершину соответственно. Чтобы это сделать, нужно построить граф кратчайших путей и посчитать на новом графе динамику (поскольку полученный граф будет ациклическим). Чтобы построить граф кратчайших путей, нужно оставить в графе только полезные ребра, предварительно запустив, например, поиск в ширину из вершин 1 и n соответственно.
После того, как величины cnt1[v] и cnt2[v] посчитаны, переберем все полезные ребра исходного графа (u, v) и к вершинам u и v прибавим величину (cnt2[u] * cnt1[v]) / (cnt2[n–1]), которая является вкладом этого ребра в искомую величину для вершин u и v. Заметим, что величина (cnt2[n–1]) — это общее количество кратчайших путей от вершины 1 до n. Все величины, которые были упомянуты, можно посчитать за размер исходного графа. Вычислительная сложность решения O(N + M).
208D - Призы, призы и еще раз призы
В этой задаче после каждого нового получения очков нужно было жадно набрать себе призов. Для этого переберем призы, начиная с самого дорогого, и попробуем взять как можно больше. Если у нас cnt очков, а текущий приз стоит p очков, то мы можем получить 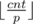 призов. Получаем простое решение за O(5 * N).
призов. Получаем простое решение за O(5 * N).
В задаче нам задан набор ориентированных вниз корневых деревьев. Сначала обойдем поиском в глубину каждое дерево в отдельности и перенумеруем вершины. Пусть размер поддерева вершины v — cnt[v].Тем самым получится, что все потомки вершины v, учитывая саму вершину v, будут иметь номера в отрезке [v;v + cnt[v]–1].
После этого будем обрабатывать запросы (v, p) по очереди. Поднимемся из вершины v запроса на p вершин вверх к корню, используя двоичный подьем, похожий на поиск lca в дереве. Пусть мы пришли в вершину u. Если у вершины нет предка на расстоянии p, сразу выводим 0, иначе нужно посчитать количество потомков полученной вершины u, которые имеют ту же высоту в дереве, что и вершина v.
Для этого, для каждой высоты выпишем в отдельный массив номера всех вершин с этой высотой. Тогда для ответа на запрос, нужно узнать, какие из вершин этого массива являются потомками нашей вершины u. Для этого можно бинарным поиском в этом массиве выделить отрезок подходящих вершин (поскольку мы знаем номера потомков вершины u) и посчитать их количество. Вычитаем из этого количества единицу (саму вершину v) и получаем ответ. Вычислительная сложность решения O(Nlog(N)) — двоичный подъем и бинарный поиск.









 Доброго Вам утра, дня, вечера, ночи.
Доброго Вам утра, дня, вечера, ночи.
