Div2 A. Параллелепипед
В этой задаче были даны площади трех граней прямоугольного параллелепипеда, нужно было найти сумму длин всех его сторон.
Пусть длины трех сторон, имеющих одну общую вершину, равны a, b и c. Тогда нетрудно видеть, что нам даны числа s1 = ab, s2 = bc и s3 = ca. Из площадей легко можно выразить длины сторон: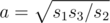 
, 
, 
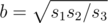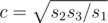. Ответом является число 4(a + b + c), поскольку в параллелепипеде есть по 4 стороны с длинами a, b и c. Сложность решения — O(1).
Div2 B. Массив
В задаче был дан массив a из n элементов, ai являлись положительными целыми и не превышали 105 для всех 1 ≤ i ≤ n. Также было дано число k. Нужно было найти минимальный по включению отрезок [l, r] такой, что среди чисел al, ... ar ровно k различных. Определение минимальности по включению дано в условии.
Заведем массив cnt, изначально элемент cnti будет равен количеству вхождений числа i в массив a. Это можно сделать, поскольку элементы массива a небольшие. Число ненулевых элементов в массиве cnt равно числу различных элементов в массиве a. Если их меньше, чем k, то искомый отрезок найти невозможно.
Допустим что это не так, тогда будем строить отрезок ответа [l, r]. Пусть изначально [l, r] = [1, n]. Будем уменьшать на 1 правую границу отрезка r, пока количество различных чисел не станет меньше, чем k. Поддерживать количество различных элементов на отрезке [l, r] можно следующим образом: при удалении элемента номер r из отрезка, уменьшим cntar на единицу. Если после этого cntar стал равным нулю, то уменьшим число различных элементов на 1. После этого вернем обратно последний выкинутый из отрезка элемент, чтобы количество различных стало ровно k. Затем сделаем точно так же с левой границей l, только будем не уменьшать, а увеличивать l на 1 каждый шаг. В результате мы получим отрезок [l, r], на котором есть ровно k различных элементов, а на отрезках [l + 1, r] и [l, r - 1] — меньше, чем k, следовательно это и есть искомый отрезок. Сложность решения — O(n).
Div2 C/Div1 A. Скобочная последовательность
В задаче была дана скобочная последовательность s из двух типов скобок. Нужно было найти правильную скобочную последовательность, являющуюся подстрокой строки s, содержащую наибольшее количество скобок <<
>>.
Для каждой открывающейся скобки попытаемся определить ей соответствующую закрывающуюся. Более формально, пусть открывающаяся скобка находится на позиции i, тогда скобка на позиции j называется ей соответствующей, если подстрока si... sj является кратчайшей правильной скобочной последовательностью, начинающейся с индекса i. Очевидно, если s не является правильной скобочной последовательностью, то не для каждой скобки найдется ей соответствующая.
Будем идти по строке s и складывать позиции, на которых находятся открывающиеся скобки, в стек. Пусть мы находимся на позиции i, если si — открывающаяся скобка, то просто положим ее номер на вершину стека. Если нет, то посмотрим на вершину стека: если стек пустой или последняя открывающаяся скобка не соответствует текущей, то очистим стек. В противном случае запомним, что для скобки, лежащей на вершине, соответствующая есть скобка на позиции j и снимем вершину со стека. Нетрудно понять, что таким образом мы найдем все соответствующие для всех скобок, если они есть.
Тогда строку s можно разбить на блоки. Блок — отрезок [l, r] такой, что скобка на позиции r — соответствующая для скобки на позиции l, и нет пары соответствующих скобок на позициях x и y таких, что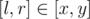 
и [l, r] ≠ [x, y]. Легко понять, что блоки не пересекаются и разбиение на блоки единственно. Мы можем склеивать подряд идущие блоки в правильные скобочные последовательности. При этом выгодно склеить как можно больше блоков, чтобы набрать как можно больше скобок нужного типа. Склеим все подряд идущие блоки, получим несколько подстрок, являющихся правильными скобочными последовательностями. Выберем из получившихся подстрок ту, в которой наибольшее количество скобок <<>>. Сложность решения — O(|s|).
Div2 D/Div1 B. Две строки
В задаче были даны две строки: s и t. Нужно было рассмотреть все вхождения строки t в строку s как подпоследовательность и сказать, верно ли, что для каждой позиции строки s найдется такое вхождение, которое содержит эту позицию.
Для каждой позиции i строки s посчитаем две величины li и ri, li — максимально возможное число такое, что строка t1... tli входит как подпоследовательность в строку s1... si, ri — максимально возможное число такое, что строка t|t| - ri + 1... t|t| входит как подпоследовательность в строку si... s|s|. Пусть мы нашли все l для позиций 1... i - 1 и хотим найти li. Если символ tli - 1 + 1 существует и совпадает с символом si, то li = li - 1 + 1, в противном случае li = li - 1. Аналогично можно найти ri, если двигаться с конца строки.
Теперь научимся проверять для позиции i в строке s, что она принадлежит хотя бы одному вхождению. Допустим, это так, и символ si соответствует символу tj в строке t. Тогда li - 1 ≥ j - 1 и ri + 1 ≥ |t| - j, по определению l и r. Тогда если существует j, такое что si = tj и li - 1 + 1 ≥ j ≥ |t| - ri + 1, то позиция i строки s принадлежит хотя бы одному вхождению t, в противном случае нет. Это легко проверить, если мы заведем для каждой буквы массив cnta, i — количество букв a в строке t на позициях 1... i. Алфавит небольшой, поэтому никаких проблем с памятью не будет. Сложность решения — O(|s| + |t|)
Div2 E/Div1 C. Частичные суммы
В задаче был дан массив a. За одну операцию массив a заменяется массивом из его частичных сумм s. Нужно было найти массив после выполнения k таких операций. Все вычисления производятся по модулю P = 109 + 7.
Запишем s в следующем виде:
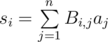
где Bi, j = 1, если i ≥ j и Bi, j = 0, если i < j, для всех 1 ≤ i, j ≤ n. Если a и s представить в виде векторов-столбцов, то применение одной операции соответствует умножению матрицы B на вектор столбец a. Тогда массив, получающийся после выполнения k операций результирующий массив будет равен Bka. Возводить матрицу в степень можно за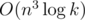 
, что уже неплохо, но недостаточно быстро.
Заметим, что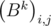 
= 
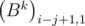, то есть элементы матрицы Bk на диагоналях, параллельным главным, одинаковы. Это можно легко доказать, используя метод математической индукции, предоставляю это читателю. Тогда можно задавать матрицу набором чисел 
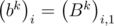, равным элементам первого столбца. Элементы первого столбца для произведения BkBl равны 
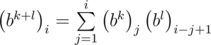. Это следует прямо из формулы умножения двух матриц. Вычисление одного элемента работает за O(n) времени, всего элементов n, поэтому умножение можно производить за O(n2). Таким образом, мы научились решать задачу за 
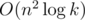времени, что уже укладывается в ограничения.
Можно решать эту задачу быстрее, если убедиться, что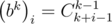 
. Допустим, что эта формула верна для какого-то k, докажем, что из этого следует, что формула верна и для k + 1. Используем формулу умножения для коэффициентов b:
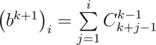
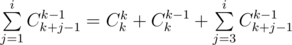
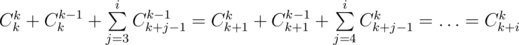
Используя формулу Cnk = n! / k!(n - k)!, можно получить, что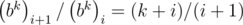 
, поэтому мы можем построить все коэффициенты b, если умеем делить по модулю P, поэтому в этом решении существенна простота P. Обратный для числа x по простому модулю равен 
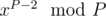в силу малой теоремы Ферма. Таким образом, мы получаем решение за O(n2).
Div1 D. Паук
В этой задаче был дан многоугольник из n вершин, нужно было найти кратчайший путь от одной его вершины до другой, если можно двигаться по границе, а также спускаться вертикально вниз, не выходя наружу.
Все стороны многоугольника можно разбить на три группы: верхние, нижние и вертикальные. Вертикальная сторона это сторона, у которой совпадают координаты x ее концов. Нижняя сторона это такая сторона, что внутренность многоугольника лежит сверху от нее. Верхняя сторона это такая сторона, что внутренность многоугольника лежит снизу от нее. Понятно, что мы можем спускаться только с точек верхних сторон в точки нижних сторон. Вертикальные стороны на спуски никак не влияют, поскольку спуск проходящий через вертикальную сторону может быть разбит на два спуска и переход. Докажем, что нужно спускаться либо из вершины либо в вершину. Допустим, что какой-то спуск в оптимальном решении начинается с внутренней точки и заканчивается внутренней точкой. Попробуем немного изменить координату x этого спуска. Поскольку длина пути монотонно (возможно нестрого монотонно) зависит от x, то можно немного сдвинуть x так, что ответ не увеличится, а может быть даже и уменьшится. Нестрогая монотонность ломается только если спуск проходит через какую-то вершину, поэтому нужно рассматривать спуски из вершин и в вершины.
Решаем задачу методом сканирующей прямой, будем двигать вертикальную прямую с абсциссой X слева направо и поддерживать множество S пересекающихся с ней сторон. Элементы этого множества будем хранить в отсортированном по y порядке. Поскольку стороны имеют общие точки только в вершинах, порядок всегда можно определить. При движении происходят разные события: какие-то отрезки добавляются в множество S, какие-то удаляются из него. Заведем массив событий, каждое событие описывается координатой x, равное координате X прямой, при котором происходит событие, а также типом события: номером отрезка и удаляется он или добавляется в S. Понятно, что для каждой стороны есть по два события, их координаты x соответствуют абсциссам концов сторон. Вертикальные стороны при этом можно игнорировать.
Будем обрабатывать события в порядке неубывания координат x этих событий. Если пришло событие добавления стороны, то добавим сторону в S, после добавления посмотрим на ближайших соседей этой стороны в текущем множестве S. Если только что добавленный отрезок верхний, то проводим спуск из его левой вершины вниз, до пересечения с нижним соседом, а именно находим точку пересечения, запоминаем на каком отрезке она находится и запоминаем, что есть спуск из вершины в эту новую точку. Если добавленная сторона нижняя, то проводим спуск с верхнего соседа в левый конец добавленного отрезка, точно так же запоминая точку пересечения, на какой стороне она лежит и то, что есть спуск из этой точки в вершину. Если же событие соответствует удалению отрезка, то мы точно так же анализируем его соседей, только спуски будут начинаться или заканчиваться в правом конце отрезка, который мы собираемся удалять. Важный момент, если у нас происходит несколько событий одного типа одновременно, мы должны их обработать также одновременно, то есть если есть несколько добавлений в одной и той же координате x, нужно добавить их всех, а только потом рассматривать соседей. Аналогично, если нужно сделать несколько удалений, нужно рассмотреть соседей и только потом удалить отрезки. Также при равенстве координат x события добавления должны идти раньше событий удаления, иначе решение не будет работать в случае двух углов, лежащих по разные стороны от вертикальной прямой, но с вершинами, лежащими на этой вертикальной прямой.
Множество S удобно хранить в контейнере типа set, при этом для него нужно аккуратно написать компаратор. Можно делать это следующим образом: Два отрезка могут одновременно находиться в S, если есть вертикальная прямая, которая пересекает каждый из них. В общем случае такая вертикальная прямая не единственная, возможные положения X, при котором это так, лежат на отрезке [l, r], который легко находится по координатам концов отрезков. Тогда можно взять произвольное X внутри [l, r] и сравнить ординаты точек пересечения. Удобно брать именно внутреннюю точку, поскольку не придется рассматривать частные случаи, связанные с тем, что сравниваемые отрезки могут иметь общий конец.
После этого строим граф, вершинами которого являются вершины многоугольника и концы возможных спусков, а ребра — отрезки сторон и спуски. Кратчайший путь на таком графе ищется алгоритмом Дейкстры. Сложность решения — 
.
Div1 E. Планарный граф
В задаче был дан связный неориентированный планарный граф, без мостов, точек сочленения, кратных ребер и петель, уложенный на плоскость. Также были даны запросы следующего типа: для заданного цикла посчитать количество вершин внутри этого цикла, либо на нем самом.
Возьмем произвольную вершину на границе, например вершину с самой маленькой абсциссой. Подвесим к ней новую вершину, причем ребро между вершиной на границе и новой вершиной должно быть снаружи от внешней грани графа. Назовем эту вершину стоком. Из каждой вершины графа, кроме стока, пустим поток величиной 1, текущий в сток. Поток можно пустить по дереву поиска в ширину или глубину, время, затрачиваемое на такую операцию есть O(E).
Рассмотрим какой-нибудь запрос. Считаем, что цикл ориентирован против часовой стрелки, если это не так, то перевернем его. Сделаем разрез в графе: в первой доле разреза будут все вершины, которые лежат внутри цикла или на нем самом, во второй доле --- все оставшиеся вершины, в том числе и сток. Докажем, что величина потока через разрез равна количеству вершин в первой доле. Очевидно, что вклад в общий поток от каждой вершины графа можно рассматривать независимо. Пусть вершина находится в первой доле. Единичный поток от нее течет к стоку по какому-то пути. Так как эта вершина и сток находятся в разных долях, то этот путь нечетное число раз проходит по ребрам разреза, поэтому вклад в поток через разрез от этой вершины равен 1. Рассмотрим вершину, находящуюся во второй доле. Так как она в той же доле, что и сток, то поток от нее до стока проходит по ребрам разреза четное число раз, поэтому вклад от нее нулевой. Чтобы найти величину потока через разрез, нужно просуммировать потоки, текущие по ребрам разреза. Заметим, что каждое ребро разреза инцидентно ровно одной вершине, лежащей на цикле, поэтому можно для каждой вершины цикла просуммировать потоки, по ребрам, ведущим из этой вершины наружу цикла. Чтобы найти все ребра, ведущие наружу, отсортируем по углу все ребра, исходящие из вершины, в порядке против часовой стрелки. Тогда все ребра, ведущие наружу из вершины цикла, будут расположены после предыдущей вершины цикла и перед следующей вершиной цикла. Поэтому сумма потоков по ребрам наружу сводится к сумме на отрезке, что успешно решается частичными суммами. Сложность решения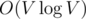 
на сортировку графа плюс 
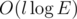на запрос, где l — длина цикла. Логарифм числа ребер возникает из-за необходимости узнавать номер вершины в списке смежности для другой вершины.
