Добрый вечер.
При решении этой несложной задачи неожиданно столкнулся с тем, что я, кажется, не понимаю, как устроена работа функции printf. А именно есть три решения: раз, два и три.
Отличия исключительно в 47-й строке.
Почему третье решение получает WA, тогда как у двух первых ОК?
Разве функция printf не должна приводить аргумент к типу, заданному форматной строкой? А если должна, то как от приведения целочисленного нуля к double возникают проблемы?
Заранее спасибо за ответы.









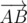 на
на 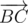 , численно равное
, численно равное 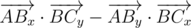 . Знак векторного произведения определяется знаком синуса ориентированного угла между векторами (т.к. векторное произведение также равно
. Знак векторного произведения определяется знаком синуса ориентированного угла между векторами (т.к. векторное произведение также равно 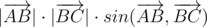 ), а именно этот-то знак нам и нужно узнать.
), а именно этот-то знак нам и нужно узнать.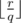
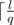
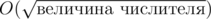 отрезков, на которых его значение постоянно. Причем мы можем найти все эти отрезки и значения за
отрезков, на которых его значение постоянно. Причем мы можем найти все эти отрезки и значения за 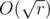 . Точнее, нас интересуют такие
. Точнее, нас интересуют такие 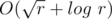 .
.
