В первом отборочном раунде 609 участников послали хотя бы одно решение и 396 послали хотя бы одно правильное решение. Задачи Неквадраты и Раздел королевства были довольно простыми, по обеим было примерно 300 правильных решений. Задача Столбики монет была относительно простой, ее решило 145 участников. Три оставшиеся задачи оказались сложнее. Задача Стикеры могла бы быть очень сложной задачей на строки, но маленький размер входных данных позволял решать задачу с помощью динамического программирования — задачу сдали 22 участника. Задачу Ассистенты решило 13 участников; в ней требовалось использование бинарного поиска, жадности и некоторых известных структур данных. Никто не смог решить за время соревнования задачу Государственные дороги, которая была изящной задачей на теорию графов с решением, которое было легко запрограммировать, но сложно придумать.
Поздравляем Kenny_HORROR, единственного участника, решившего 5 задач. Также поздравляем Petr, tourist и eatmore, которые решили 4 задачи с отрицательным штрафным временем и прошли в финал.
Задачи этого раунда подготовлены польской командой: Tomasz Idziaszek ( Раздел королевства ), Jakub Łącki ( Государственные дороги ), Marcin Pilipczuk ( Ассистенты ), и Jakub Radoszewski ( Неквадраты, Столбики монет ). Отдельное спасибо профессору Costas Iliopoulos за идею задачи Стикеры.
Решения, тесты и разбор были подготовлены marek.cygan, monsoon и jakubr.
Задача A (Ассистенты)
В этой задаче нам нужно найти минимальное количество дней, за которые можно завершить n исследовательских задач. Профессор может выполнить i-ю задачу за pi последовательных дней, либо передать ее ассистенту, который выполнит ее за ai последовательных дней. Каждый ассистент может выполнить только одну задачу, и профессору требуется один день на поиск ассистента.
Мы покажем, как проверить, можно ли завершить весь проект за k дней. Затем остается только использовать бинарный поиск по ответу.
Легко видеть, что существует оптимальное расписание, в котором профессор сначала ищет ассистентов, а потом выполняет задачи, которые никому не передал. Кроме того, это означает, что нам не нужно беспокоиться о том, чтобы профессор выполнял свои задачи в последовательные дни. Формально говоря, если есть некоторое оптимальное расписание, в котором профессор передает подмножество задач 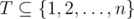 ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества T в течение первых #T дней, а потом выполняет все оставшиеся задачи сам, каждую задачу — в непрерывную последовательность дней. Таким образом, если профессор передаст задачи из T, он закончит оставшиеся задачи в срок тогда и только тогда, когда
ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества T в течение первых #T дней, а потом выполняет все оставшиеся задачи сам, каждую задачу — в непрерывную последовательность дней. Таким образом, если профессор передаст задачи из T, он закончит оставшиеся задачи в срок тогда и только тогда, когда 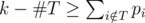 .
.
Теперь приведем алгоритм, который будет проверять, существует ли такое T. Рассмотрим дни d = k, k - 1, ..., 1 в обратном хронологическом порядке, и в некоторые из этих дней мы будем передавать задачи ассистентам. Предположим, что на день d мы уже передали подмножество задач 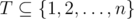 за дни после d. Пусть
за дни после d. Пусть 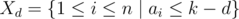 — множество задач, которые могут быть переданы в день d таким образом, что ассистент успеет выполнить их в срок. Главное наблюдение состоит в следующем: если
— множество задач, которые могут быть переданы в день d таким образом, что ассистент успеет выполнить их в срок. Главное наблюдение состоит в следующем: если 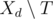 непусто, то мы можем в день d жадным образом передать задачу
непусто, то мы можем в день d жадным образом передать задачу 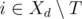 , которая максимизирует значение pi.
, которая максимизирует значение pi.
Теперь докажем, что алгоритм работает правильно. Предположим, что существует расписание S, которое в течение дней после d совпадает с нашим. Если в расписании S задача i передается ассистенту в день d, то все хорошо. Иначе в расписании S в день d профессор либо передает задачу j ≠ i ассистенту, либо выполняет задачу j сам (в последнем случае, возможно, j = i).
В первом случае профессор передает асистенту задачу j ≠ i. Тогда 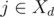 (так как ассистент выполнит задачу в срок) и
(так как ассистент выполнит задачу в срок) и 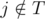 (мы предполагаем, что расписание S совпадает с нашим планом после дня d). Благодаря нашему жадному выбору имеем pi ≥ pj. Если в S профессор передает ассистенту задачу i в день d', то d' ≤ d (так как
(мы предполагаем, что расписание S совпадает с нашим планом после дня d). Благодаря нашему жадному выбору имеем pi ≥ pj. Если в S профессор передает ассистенту задачу i в день d', то d' ≤ d (так как 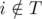 и S совпадает с нашим планом в последующие дни), и мы можем в S переставить дни, в которые мы передаем ассистентам задачи i и j. Иначе, если в S профессор выполняет задачу i самостоятельно, мы можем изменить S следующим образом: мы передаем ассистенту задачу i в день d и выполняем задачу j в те дни, в которые профессор ранее выполнял задачу i (мы можем так сделать, потому что pi ≥ pj).
и S совпадает с нашим планом в последующие дни), и мы можем в S переставить дни, в которые мы передаем ассистентам задачи i и j. Иначе, если в S профессор выполняет задачу i самостоятельно, мы можем изменить S следующим образом: мы передаем ассистенту задачу i в день d и выполняем задачу j в те дни, в которые профессор ранее выполнял задачу i (мы можем так сделать, потому что pi ≥ pj).
Во втором случае профессор выполняет задачу j в день d. Если j = i, профессор может вместо этого передать ассистенту эту задачу в день d (так как 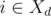 ). Иначе, если j ≠ i, профессор может передать задачу i в день d и вернуть пропущенный день, выполнив задачу j в момент, в который профессор работал над задачей i (передавая или выполняя ее) в расписании S.
). Иначе, если j ≠ i, профессор может передать задачу i в день d и вернуть пропущенный день, выполнив задачу j в момент, в который профессор работал над задачей i (передавая или выполняя ее) в расписании S.
Во всех случаях мы получаем оптимальное расписание, в котором профессор делеигрует задачу i в день d, таким образом основное наблюдение доказано.
Как быстро мы можем реализовать данный алгоритм? Выбор максимума в множестве 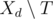 может быть реализован с помощью бинарной кучи, отсортированной по pi. Переходя от дня d + 1 к дню d, мы добавляем элементы из
может быть реализован с помощью бинарной кучи, отсортированной по pi. Переходя от дня d + 1 к дню d, мы добавляем элементы из 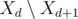 в кучу (то есть задачи с ai = k - d; для этого нужно отсортировать задачи по ai) и удаляем максимальный элемент (и добавляем его в T).
в кучу (то есть задачи с ai = k - d; для этого нужно отсортировать задачи по ai) и удаляем максимальный элемент (и добавляем его в T).
Заметим, что нам не нужно проходить по всем дням, мы можем начать с дня d = min(k, n), так как нет нужды передавать задачи ассистентам после n-го дня. Таким образом, все решение (с фиксированным k) работает за время  .
.
Мы можем улучшить его, если будем перебирать не дни, а задачи, отсортированные по невозрастанию pi. Каждый раз мы будем пытаться передать задачу i в самый последний день из {1, 2, ..., di}, где di = min(k - ai, n)}, в который еще ни одна задача не передается. Несложно видеть, что полученное множество T будет таким же, как в предыдущем алгоритме. Эта операция выбора последнего свободного дня может быть выполнена за почти линейное время, используя структуру леса непересекающихся множеств. Каждое множество содержит свободный день d и все дни после него, в которые какие-то задачи передаются. Теперь выбор последнего свободного дня сводится к нахождению множества, которое содержит di, получения минимального элемента d' в этом множестве, передаче задачи i ассистенту в день d' и объединению данного множества с множеством, содержащим элемент d' - 1.
Давайте теперь оценим окончательную временную сложность. Так как одним из решений является передача всех задач ассистентам, ответ всегда будет меньше, чем n + A, где A = maxiai. Добавляя бинарный поиск, мы получаем решение, работающее за время 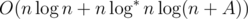 .
.
Задача B (Раздел королевства)
В этой задаче нам нужно разделить сетку n × m на максимальное количество частей различных размеров, являющиеся связными компонентами, состоящими из единичных квадратов. Мы должны представить пример такого разделения, используя буквы из множества  для обозначения получающихся частей. Решение этой задачи получается в три шага.
для обозначения получающихся частей. Решение этой задачи получается в три шага.
На первом шаге мы забудем на время про требование связности и определим, какие размеры частей приведут к максимальному результату. Ответ прост: части должны иметь размеры 1, 2, 3, ... Если последняя часть меньше требуемого, мы объединяем ее с предпоследней частью.
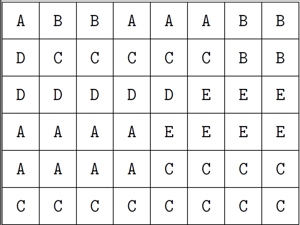
На втором шаге мы заметим, что всегда возможно получить разделение, полученное на предыдущем шаге. Мы можем покрыть всю сетку змеевидным маршрутом, затем разрезать змейку в соответствующих позициях — получившиеся части будут связными и будут иметь нужные размеры, см. картинку слева.
На третьем шаге мы разметим части буквами из множества  так, что никакие две соседние части не будут размечены одинаковыми буквами. Кажется привлекательной идея пометить их буквами
так, что никакие две соседние части не будут размечены одинаковыми буквами. Кажется привлекательной идея пометить их буквами 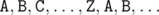 в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает.
в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает.
Одно из возможных правильных решений состоит в том, чтобы пометить каждую часть наименьшей буквой из тех, что еще не встречаются среди пометок ее соседей (и помечать части змейки по порядку). Другая идея состоит в том, чтобы помечать части в первом ряду буквами A и B, во втором ряду использовать C и D, в третьем — E и F, в четвертом снова A и B и так далее (см. картинку справа). Начиная с момента, когда каждая часть покрывает хотя бы один ряд целиком, мы можем начать использовать только две буквы, A и B. Во втором способе мы используем только 6 различных букв.
Интересная задача — определить, каково минимальное количество букв, достаточное для того, чтобы разметить любую сетку.
Вышеприведенный алгоритм может быть легко реализован с временной сложностью O(nm).
Задача C (Неквадраты)
В этой задаче нам нужно проверить, может ли данное положительное целое число n быть представлено в виде произведения k положительных целых чисел, ни одно из которых не является квадратом целого числа. Давайте назовем такое представление неквадратным представлением.
Общий подход к задаче — динамическое программирование по множеству делителей n. Все делители n можно найти за время  . Пусть D(n) — число делителей n. Оказывается, для n ≤ 109 верно D(n) ≤ 1344.
. Пусть D(n) — число делителей n. Оказывается, для n ≤ 109 верно D(n) ≤ 1344.
Мы вычислим двумерную булеву матрицу 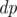 , где
, где 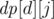 — истина если и только если делитель d может быть представлен в виде произведения j неквадратов. При вычислении используется следующая булева формула, которяа работает при j ≥ 1 и
— истина если и только если делитель d может быть представлен в виде произведения j неквадратов. При вычислении используется следующая булева формула, которяа работает при j ≥ 1 и 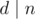 :
:
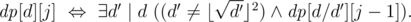
Временная сложность этого решения составляет 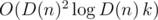 (логарифм появляется из-за использования структуры map или аналогичной для хранения делителей n. Сложность по памяти составляет O(D(n)k).
(логарифм появляется из-за использования структуры map или аналогичной для хранения делителей n. Сложность по памяти составляет O(D(n)k).
Можно улучшить время работы этого решения, если заметить, что параметр k ограничен сверху числом 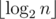 , что в нашем случае не более 29. Действительно, для
, что в нашем случае не более 29. Действительно, для 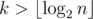 ответ всегда «NO» (доказательство следует из следующего решения).
ответ всегда «NO» (доказательство следует из следующего решения).
Есть также гораздо более простое решение, которое рассматривает разложение n на простые множители. Пусть n = p1α1p2α2... pmαm, где pi — различные простые числа. Тогда решение состоит в следующем:
- Если α1 + α2 + ... + αm < k, вывести «NO».
- Иначе, если m > 1, вывести «YES».
- В оставшемся случае m = 1. Если k - α1 четно, вывести «YES», иначе вывести «NO».
Обоснуем это решение. Ответ в случае (1) следует из того факта, что у любого делителя-неквадрата есть простой делитель. Для m = 1 нам нужно просто проверить, может ли α1 быть представлено как сумма k нечетных целых чисел, что возможно тогда и только тогда, когда четность k и α1 совпадает. Это дает пункт (3) алгоритма.
Наконец, рассмотрим пункт (2). Нам нужно показать, что, если α1 + α2 + ... + αm ≥ k и m > 1, то существует неквадратное представление n. Давайте возьмем в качестве первых k - 1 неквадратов простые делители n: сначала α1 раз делитель p1, затем α2 раз делитель p2 и так далее. В качестве последнего делителя, d, мы возьмем произведение оставшихся простых делителей. Если d не является квадратом целого числа, мы построили требуемое представление. Иначе мы заменим последний делитель на d / pm, а первый делитель — на p1 pm, таким образом получая требуемое представление.
Это решение требует только найти разложение n на простые множители и работает за время  .
.
Задача D (Столбики монет)
В этой задаче m золотых и серебряных монет разложены в n кучек разной высоты. Нам нужно перераспределить монеты таким образом, чтобы образовалось максимальное количество одноцветных кучек (в одноцветной куче либо все монеты золотые, либо все монеты серебряные). Нам разрешается выполнить сколько угодно операций перестановки двух монет, которые находятся на одинаковой высоте в разных кучках.
Пусть k — ответ, то есть максимальное количество одноцветных кучек, которого можно достичь. Выполним бинарный поиск по k. С этого момента нам остается научиться отвечать на следующий вопрос: для данного k проверить, можно ли получить k одноцветных кучек. Очевидно, оптимально попытаться сделать k самых маленьких кучек одноцветными.
Так как количество операций не ограничено, нашу задачу можно переформулировать следующим образом. Пусть h — высота k-й минимальной кучки. Для каждого уровня высоты 1, ..., h мы знаем общее количество золотых и серебряных монет на этом уровне. Нам нужно проверить, достаточно ли этих чисел, чтобы сформировать k одноцветных кучек. Эта задача будет сведена к подсчету пересечения O(h) отрезков.
Для начала рассмотрим каждый уровень по отдельности. Предположим, что нам этом уровне есть gi золотых и si серебряных монет, а k минимальных кучек содержат в сумме ti монет на этом уровне. Используя эти числа, мы можем рассчитать отрезок [ai, bi] такой, что 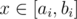 тогда и только тогда, когда возможно добиться того, чтобы на i-м уровне выбранных кучек оказалось в сумме x золотых и ti - x серебряных монет. Отметим, что отсюда будет следовать, что аналогичный отрезок для возможного количества серебряных монет на i-м уровне — это [ti - bi, ti - ai].
тогда и только тогда, когда возможно добиться того, чтобы на i-м уровне выбранных кучек оказалось в сумме x золотых и ti - x серебряных монет. Отметим, что отсюда будет следовать, что аналогичный отрезок для возможного количества серебряных монет на i-м уровне — это [ti - bi, ti - ai].
Теперь нам нужно убедиться, что отрезки для разных уровней позволяют нам найти корректное решение. Мы пройдем от самого нижнего к самому верхнему уровню. На уровня i нам нужно пересечь отрезок [ai, bi] с [ai - 1, bi - 1] и аналогично отрезки для количества серебряных монет. Таким образом мы получим один обновленный отрезок [ai, bi], который мы далее будем использовать для обновления отрезков на более высоких уровнях.
Это решение работает за время 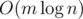 .
.
У этой задачи также есть решение за линейное время. Пусть gi — общее количество золотых монет, которые находятся на i-м уровне. Пусть g'i — максимальное количество кучек, которые можно сформировать таким образом, чтобы у них у всех были только золотые монеты на i-м уровне и ниже. Можно легко вычислить g'i при помощи следующего рекуррентного соотношения:
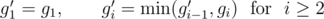
Аналогично мы определяем si и s'i для серебряных монет.
Пусть hi — высота i-й кучки, и предположим, что кучки отсортированы по невозрастанию высоты, то есть h1 ≥ h2 ≥ ... ≥ hn. Мы пройдем по кучкам и «раскрасим» их (делая их одноцветным), когда это возможно. Пусть мы рассматриваем i-ю кучку, и мы уже раскрасили кучки с номерами 1, 2, ..., i - 1 таким образом, что всего есть G золотых кучек и S серебряных.
Мы можем сделать i-ю кучку золотой, если и только если g'hi > G. В таком случае мы покажем, что существует оптимальное решение, в котором эта кучка сделана золотой, а кучки 1, 2, ..., i - 1 раскрашены так же, как в нашем решении. Рассмотрим произвольное оптимальное решение, в котором кучки 1, 2, ..., i - 1 раскрашены так же, как в нашем решении. Пусть j ≥ i — самая высокая золотая кучка в этом оптимальном решении (она должна существовать, иначе мы можем добавить i-ю кучку и получить решение лучше). Можно поменять местами монетки из j-й кучки и i-й кучки и, так как g'hj + 1 ≥ g'hi > G, у нас есть достаточно много золотых монет, чтобы поместить их в i-ю кучку выше уровня hj.
Аналогично, если мы не можем сделать i-ю кучку золотой, но можем сделать ее серебряной (то есть s'hi > S), существует оптимальное решение, в котором мы так и делаем.
Иначе g'hi + s'hi ≤ G + S, что означает, что мы не можем «раскрасить» более чем G + S кучек высоты не менее hi.
Так как мы можем отсортировать кучки по высоте с помощью сортировки подсчетом, описанный алгоритм работает за время O(n + m).
Задача E (Государственные дороги)
В этой задаче нам дан динамически изменяющийся граф. Множество его вершин зафиксировано, но ребра добавляются и удаляются с течением времени. Нам нужно отвечать на запросы следующего вида: может ли подмножество вершин 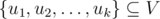 представлять собой одну или более связных компонент графа в данный момент времени.
представлять собой одну или более связных компонент графа в данный момент времени.
Мы представим рандомизированное решение этой задачи, которое легко запрограммировать, но довольно сложно придумать. Для каждого ребра, добавляемого в граф, мы выберем случайный целый вес. Для каждой вершины 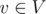 мы храним в ячейке массива
мы храним в ячейке массива 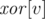 результат операции
результат операции 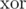 , примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время O(1) при добавлении и удалении ребер.
, примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время O(1) при добавлении и удалении ребер.
Главное наблюдение состоит в том, что множество вершин {u1, u2, ..., uk} представляет собой набор связных компонент тогда и только тогда, когда каждое ребро графа инцидентно либо двум, либо ни одной из вершин ui. Таким образом, чтобы ответить на запрос, мы вычисляем:
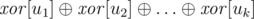
где  обозначает операцию
обозначает операцию 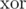 . Если полученное значение не равно нулю, мы знаем, что ответ — «NO». Иначе с высокой вероятностью ответ — «YES». Вероятность неправильного положительного ответа —
. Если полученное значение не равно нулю, мы знаем, что ответ — «NO». Иначе с высокой вероятностью ответ — «YES». Вероятность неправильного положительного ответа — 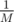 , где M — максимальный вес ребра. Эта вероятность оказывается достаточно мала при M = 232 или M = 264.
, где M — максимальный вес ребра. Эта вероятность оказывается достаточно мала при M = 232 или M = 264.
Все решение работает за линейное время от размера входных данных.
Задача F (Стикеры)
В этой задаче нам дано n видов сткеров s1, ..., sn, где каждое si является словом длины d. Нас просят найти минимальное количество стикеров, которые нужны, чтобы составить данное слово t длины m.
Мы предложим простое решение, основанное на динамическом программировании. Обозначим как dp[i] минимальное количество стикеров, необходимое для того, чтобы составить ровно суффикс t[i..m], а как  такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из t[i - d..i - 1] (но не обязательно при этом правильными буквами). Ответ к задаче — это dp[1].
такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из t[i - d..i - 1] (но не обязательно при этом правильными буквами). Ответ к задаче — это dp[1].
Как посчитать dp[i]? Ясно, что i-я позиция t должна быть в какой-то момент покрыта стикером, который начинается в этой позиции. Так как все стикеры имеют одинаковую длину, мы можем ограничить себя тем, чтобы положить этот стикер самым первым или самым последним. Это дает нам два случая:
- Для некоторого j имеем sj = t[i..i + d - 1]. Тогда мы можем составить суффикс t[i + d..m], возможно накрывая некоторые буквы из t[i..i + d - 1], и затем положить стикер sj, начиная с позиции i. В этом случае мы используем
 стикеров.
стикеров. - Имеем sj[1..d'] = t[i..i + d' - 1] для некоторого j и некоторого d' ≤ d. Тогда мы можем положить sj, начиная с позиции i, затем составить t[i + d'..m] с ограничением, что нам нельзя изменять буквы перед позицией i + d'. В этом случае мы используем 1 + dp[i + d'] стикеров.
Если для каждого i мы знаем максимальное l[i], такое что t[i..i + l[i] - 1] является префиксом некоторого стикера, то случай (1) возможен, когда d = l[i], и результат случая (2) равен min1 ≤ j ≤ l[i](1 + dp[i + j]).
Мы вычисляем  аналогично, но теперь вместо множества всех стикеров мы рассмотрим множество всех суффиксов стикеров. Таким образом мы вычисляем l[i] как максимальное число, такое что t[i..i + l[i] - 1] является подстрокой некоторого стикера.
аналогично, но теперь вместо множества всех стикеров мы рассмотрим множество всех суффиксов стикеров. Таким образом мы вычисляем l[i] как максимальное число, такое что t[i..i + l[i] - 1] является подстрокой некоторого стикера.
Это решение может быть реализовано с временной сложностью O(mnd2). Интересно, что эта задача может быть решена за линейное время от размера входа, даже с использованием стикеров разной длины, но это решение гораздо сложнее.










 . Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст
. Иначе рассмотрим, какой ожидаемый вклад в изменение настроения даст 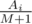 . Для невкусных конфет ожидаемый вклад в изменение настроения равен
. Для невкусных конфет ожидаемый вклад в изменение настроения равен 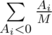 , так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно
, так как первой невкусной конфетой может оказаться равновероятно любая из невкусных. В итоге математическое ожидание изменения настроения равно 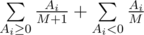 .
.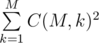 .
.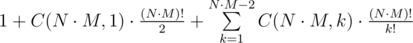 .
.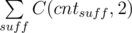 , где суммирование ведётся по всем суффиксам.
, где суммирование ведётся по всем суффиксам.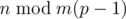 — хорошее. Рассчитаем и запомним в таблице для каждого
— хорошее. Рассчитаем и запомним в таблице для каждого 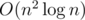 .
.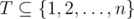 ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества
ассистентом и выполняет остальные задачи сам (но необязательно в последовательные дни), то существует оптимальное расписание, в котором профессор передает задачи из подмножества 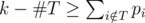 .
.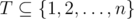 за дни после
за дни после 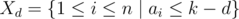 — множество задач, которые могут быть переданы в день
— множество задач, которые могут быть переданы в день 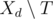 непусто, то мы можем в день
непусто, то мы можем в день 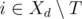 , которая максимизирует значение
, которая максимизирует значение 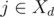 (так как ассистент выполнит задачу в срок) и
(так как ассистент выполнит задачу в срок) и 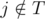 (мы предполагаем, что расписание
(мы предполагаем, что расписание 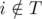 и
и 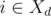 ). Иначе, если
). Иначе, если 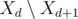 в кучу (то есть задачи с
в кучу (то есть задачи с  .
.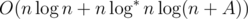 .
. для обозначения получающихся частей. Решение этой задачи получается в три шага.
для обозначения получающихся частей. Решение этой задачи получается в три шага.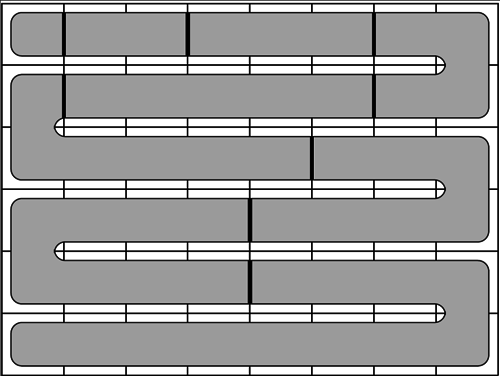
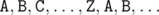 в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает.
в том порядке, в котором части появляются на змейке. Однако в некоторых случаях такой способ не работает. . Пусть
. Пусть 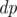 , где
, где 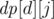 — истина если и только если делитель
— истина если и только если делитель 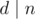 :
: 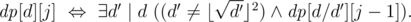
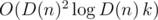 (логарифм появляется из-за использования структуры map или аналогичной для хранения делителей
(логарифм появляется из-за использования структуры map или аналогичной для хранения делителей 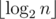 , что в нашем случае не более 29. Действительно, для
, что в нашем случае не более 29. Действительно, для 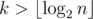 ответ всегда «NO» (доказательство следует из следующего решения).
ответ всегда «NO» (доказательство следует из следующего решения).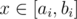 тогда и только тогда, когда возможно добиться того, чтобы на
тогда и только тогда, когда возможно добиться того, чтобы на 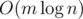 .
.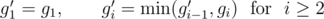
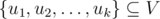 представлять собой одну или более связных компонент графа в данный момент времени.
представлять собой одну или более связных компонент графа в данный момент времени.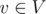 мы храним в ячейке массива
мы храним в ячейке массива 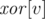 результат операции
результат операции 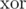 , примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время
, примененной к весам всех ребер, инцидентных этой вершине. Заметим, что такие значения можно обновлять за время 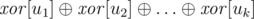
 обозначает операцию
обозначает операцию 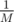 , где
, где  такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из
такое же число, но при этом разрешим стикерам выходить за границу и накрывать позиции из  стикеров.
стикеров.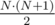 .
. . Существует быстрый способ посчитать
. Существует быстрый способ посчитать 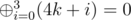 . Значит,
. Значит, 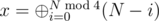 .
. . Значит, чтобы из кучки
. Значит, чтобы из кучки 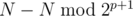 , их ровно половина. Если в
, их ровно половина. Если в 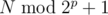 .
.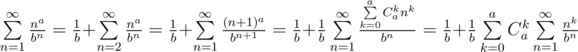
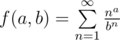 , имеем
, имеем 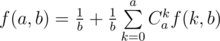
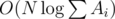 . Также следует учесть, что нужно предварительно отсортировать темы по значению
. Также следует учесть, что нужно предварительно отсортировать темы по значению 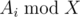 для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по
для поиска тем с максимальным количеством задач, когда у Гены уже нет возможности решать по 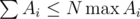 , и свойств логарифма, получается
, и свойств логарифма, получается 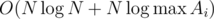 .
.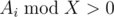 .
.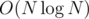 .
.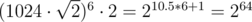 , и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...
, и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...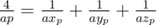 . Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для
. Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для 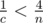 , то
, то 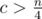 . Так как
. Так как 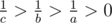 , а значит
, а значит 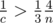 , тем самым
, тем самым 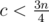 ; из аналогичных соображений
; из аналогичных соображений 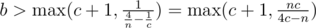 и
и 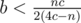 . Соответственно, перебираем для всех простых
. Соответственно, перебираем для всех простых 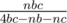 . При этом размер кода не будет превосходить 50k, что меньше, чем source limit.
. При этом размер кода не будет превосходить 50k, что меньше, чем source limit. в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).
в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).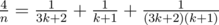 ,
,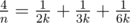 ,
,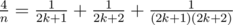 ,
,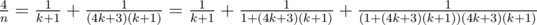 ,
,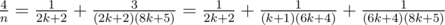 .
.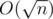 . Можно также изначально разложить число
. Можно также изначально разложить число 








