Добрый вечер!
Недавно я столкнулся со следующей проблемой: в процессе решения некой задачи мне понадобилось считать определитель достаточно специфичной матрицы:
1) Ее размер может быть до 600.
2) Все ее элементы — целые числа из множества { - 1, 0, 1}.
3) В любой ее строке и столбце не более 4 ненулевых элементов — то есть, она сильно разрежена (вообще говоря, это матрица смежности некого двудольного графа, но некоторые ребра взяты с минусом).
Притом определители надо подсчитать приблизительно у сотни таких матриц.
Я скопировал код с e-maxx.ru, и переписал все на Java, но сомневаюсь в эффективности полученного кода. Детерминант, очевидно, может быть очень большим, из-за чего приходится пользоваться BigDecimal и BigInteger с округлениями. По всем этим причинам код работает жутко медленно и нуждается в оптимизации.
public static BigInteger determinant(final int[][] matr) {
int accuracy = 20;
BigDecimal EPS = BigDecimal.valueOf(0.00000000001);
int n = matr.length;
BigDecimal[][] a = new BigDecimal[n][n];
for (int i = 0; i < n; ++i)
for (int j = 0; j < n; ++j) {
a[i][j] = new BigDecimal(matr[i][j]);
a[i][j].setScale(accuracy, BigDecimal.ROUND_HALF_UP);
}
BigDecimal det = new BigDecimal(1.0);
det.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
for (int i = 0; i < n; ++i) {
int k = i;
for (int j = i + 1; j < n; ++j)
if (a[j][i].abs().compareTo(a[k][i].abs()) > 0)
k = j;
if (a[k][i].abs().compareTo(EPS) < 0) {
det = new BigDecimal(0.0);
det.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
break;
}
BigDecimal[] tmp = a[i];
a[i] = a[k];
a[k] = tmp;
if (i != k)
det = det.divide(new BigDecimal(-1), accuracy, BigDecimal.ROUND_HALF_UP);
det = det.multiply(a[i][i]);
for (int j = i + 1; j < n; ++j)
a[i][j] = a[i][j].divide(a[i][i], accuracy, BigDecimal.ROUND_HALF_UP);
for (int j = 0; j < n; ++j)
if (j != i && a[j][i].abs().compareTo(EPS) > 0)
for (int kk = i + 1; kk < n; ++kk) {
BigDecimal aikji = new BigDecimal(1.0);
aikji.setScale(accuracy, BigDecimal.ROUND_HALF_UP);
aikji = aikji.multiply(a[i][kk]);
aikji = aikji.multiply(a[j][i]);
aikji = aikji.multiply(new BigDecimal(-1));
a[j][kk] = a[j][kk].add(aikji);
}
}
det = det.abs();
det = det.add(new BigDecimal(0.00001));
return det.abs().toBigInteger();
}
На Java я начал писать сравнительно недавно, и, возможно, упускаю какие-то моменты для оптимизации. Может ли кто-нибудь дать совет по коду, или привести ссылку на уже реализованный оптимизированный алгоритм?
UPD. Из всех предложенных вариантов подошел следующий: так как для матрицы размера N × N ответ не превосходит 2N, то можно привести матрицу к верхнетреугольному виду, выполняя все вычисления по модулю prime, где prime — простое число битовой длины не менее N — найти его помогут встроенные функции BigInteger. Скорость по сравнению с реализацией на BigDecimal возросла чуть ли не в десяток раз.
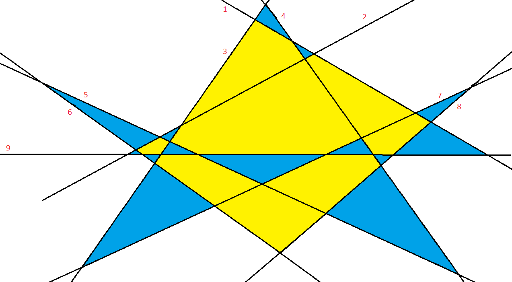
Вот такие картинки получились благодаря алгоритму (увы, смазанные на этом сайте) :)
Код, если кому-то будет интересен:
public static BigInteger determinant(final int[][] matr) {
int n = matr.length;
BigInteger[][] a = new BigInteger[n][n];
for (int i = 0; i < n; ++i) {
for (int j = 0;j < n; ++j) {
a[i][j] = BigInteger.valueOf(matr[i][j]);
}
}
BigInteger prime = BigInteger.probablePrime(n + 4, new Random());
BigInteger det = BigInteger.ONE;
for (int row = 0; row < n; ++row) {
int currentRow = row;
while (currentRow < n && a[currentRow][row].equals(BigInteger.ZERO)) {
++currentRow;
}
if (currentRow == n) {
return BigInteger.ZERO;
}
if (currentRow != row) {
det = det.negate();
BigInteger[] tmp = a[currentRow];
a[currentRow] = a[row];
a[row] = tmp;
}
BigInteger inverse = a[row][row].modInverse(prime);
for (currentRow = row + 1; currentRow < n; ++currentRow) {
if (a[currentRow][row].equals(BigInteger.ZERO)) {
continue;
}
BigInteger coefficient = a[currentRow][row].multiply(inverse).remainder(prime);
for (int column = row; column < n; ++column) {
a[currentRow][column] = a[currentRow][column].subtract(a[row][column].multiply(coefficient).remainder(prime)).remainder(prime);
}
}
}
for (int i = 0; i < n; ++i) {
det = det.multiply(a[i][i]).remainder(prime);
}
det = det.add(prime);
det = det.remainder(prime);
if (det.multiply(BigInteger.valueOf(2)).compareTo(prime) > 0) {
det = prime.subtract(det).remainder(prime);
}
return det;
}
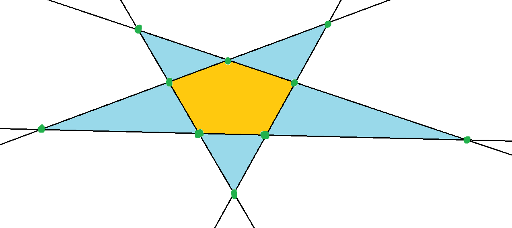
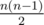и 
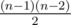— собственно, это и дает тривиальнейшую оценку на количество треугольников как что-то порядка 
.
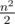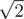, как показывает несложный анализ). 
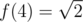достигается на очень простой конфигурации — надо поместить четыре точки в вершины куба через одну. И тут мне стало интересно — а как посчитать 
.
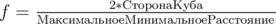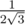(это половина диагонали куба со стороной 
) от полученных точек, поэтому вокруг каждой мы можем нарисовать куб, и считать, что точки из самой удачной конфигурации лежат в этом кубе. На следующей итерации мы делим получившиеся кубики на меньшие (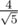
. Соответственно, самая выгодная расстановка 
