Description: A set of points P and a set of target points M in 2D space are given,. For each point M[i] in M, find the minimum angle at M[i] such that all the points P[i] in P are contained within this angle. If the angle is not less than 180 degrees, then you just have to output “TOO WIDE”.
Constraints: 1<= N,Q <=100000
My approach: First I find the convex hull and then check if the query point is in the convex hull. If it is in the polygon then the answer will be "TOO WIDE" . If not then I do as follows:
Find the centroid of the polygon and then find the angle of the vector "centroid to Pi" with x axis, where Pi represent points of the convex polygon.
Eg. if centroid =(0,0) and Pi=(1,1) is one of the points of polygon then the angle of the centroid to Pi vector is 45 degree. If Pi=(-1,-1) then the angle = 225 degree.
Then sort the points with respect to their angle. When I got a query point M then I again calculate the angle of the vector "centroid to query point M". Now I cut the polygon into two half with the line passes through the centroid and M. Then for each half I do ternary search and finally find the point X and Y as shown in the figure.
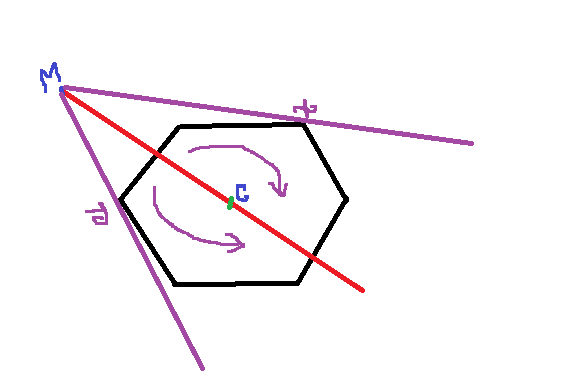
[In figure , C=centroid , M=query point and black lines represent the convex polygon]
Thus I find the angle (X,M,Y). But my approach is seemed to be incorrect and I cannot figure out what I do wrong here. Was my approach correct? Is there any other approach to solve this problem?
-Thanks in advance.










