I wonder if we can solve this problem ?
Given a DAG $$$(n <= 3e5, m <= 3e5)$$$ and $$$Q$$$ queries $$$(Q <= 3e5)$$$ $$$u$$$ $$$v$$$, determine if $$$u$$$ is ancestor of $$$v$$$ in DAG
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
I wonder if we can solve this problem ?
Given a DAG $$$(n <= 3e5, m <= 3e5)$$$ and $$$Q$$$ queries $$$(Q <= 3e5)$$$ $$$u$$$ $$$v$$$, determine if $$$u$$$ is ancestor of $$$v$$$ in DAG
I was wondering if we could implement Prim's algo in O(n log n) (n is number of vertices)
Hi guys.
I have a problem want to ask you guys.
Problem: Given a tree with n nodes, m segments in a tree with 2 endpoints. Find the maximum number of segments satisfy that not exist two segments with the edge intersect. (n < 1e3, m < 1e5);
My solution (WA passed 4/5) is: Sort m segments by the depth of their LCA. If two segments have the same LCA, if one of them have the endpoint equal to their LCA i choose it ,else i choose the one have shorter length. After sorted, i pick it one by one.
My sub For example:
n = 6, m = 4;
edges:
1 2
2 3
3 4
3 5
3 6
segments:
1 3
4 5
5 6
6 4
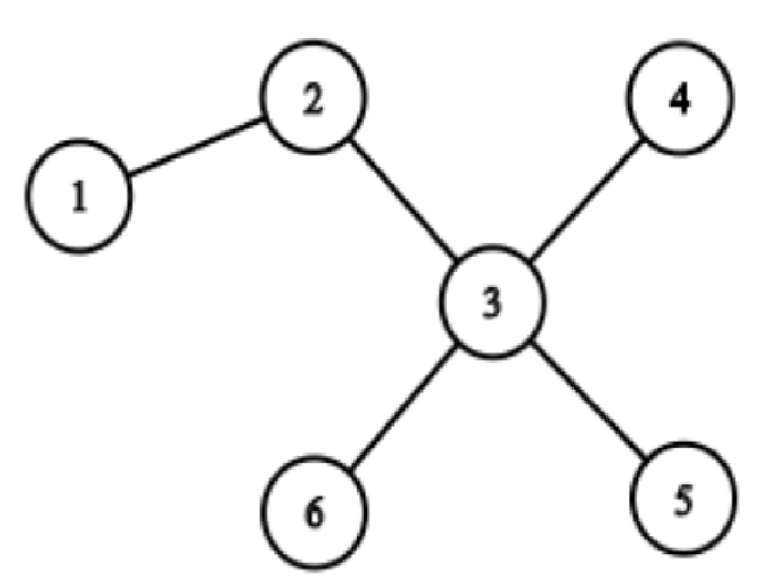
So the answer is 2 because we can choose segment (1, 3) and segment (4, 5) as path 1 -> 3 = 1 -> 2 -> 3, path 4 — > 5 = 4 — > 3 -> 5.
You also can choose (1, 3), (5, 6) or (1, 3), (6, 4)
| Название |
|---|


