Привет! Я получил хороший отлкик от сообщества Codeforces, поэтому я начинаю серию обучающих постов.

Сегодня я хочу рассказать об одной очень полезной классификации задач на динамическое программирование, к которой я пришёл за годы практики. Я не претендую на авторство этой идеи, но я ни разу не видел, чтобы она где-то явно выражалась, так что я введу собственные термины. Назовём это "ДП по подзадачам" (или "Обычное ДП") и "ДП с симуляцией процесса". Сегодня я сосредоточусь на последнем.

Обычный подход

Как вам рассказали о ДП? В каких терминах? Когда я учился в школе, мне объяснили, что ДП – это просто разбиение задачи на подзадачи. Сначала вы вводите параметры в задачу. Набор значений по каждому параметру называется состоянием ДП, оно соответствует конкретной подзадаче. Затем вам всего лишь надо найти ответ для каждого состояния / подзадачи, и знание ответа для меньших подзадач должно помочь вам найти ответ для текущей. Рассмотрим пример:

AtCoder DP Contest: Задача L Два игрока играют на массиве чисел. Они по очереди берут либо самый левый, либо самый правый из оставшихся элементов массива, пока он не опустеет. Каждый старается максимизировать сумму взятых им элементов. Какая будет разница между счетами первого и второго игроков, если они играют оптимально?

Чтобы решить эту задачу, нужно ввести два параметра: l и r, где dp[l][r] – это ответ на эту же самую задачу, но если бы мы рассматривали только числа с полуинтервала [l, r). Как его посчитать? Вы просто сводите задачу к её подзадачам. Есть два возможных хода первого игрока: взять самое левое число или самое правое число. В первом случае остаётся полуинтервал [l + 1, r), во втором случае – полуинтервал [l, r - 1). Но если мы считаем значение dp по всем полуинтервалам в порядке возрастания длины, то к этому моменту мы уже знаем исход игры в обоих случаях: это a[l] - dp[l + 1][r] и a[r - 1] - dp[l][r - 1]. И так как первый игрок хочет максимизировать разницу, то он выберет максимальное из этих двух чисел, значит итоговая формула — dp[l][r] = max(a[l] - dp[l + 1][r], a[r - 1] - dp[l][r - 1]).

Здесь объясенние через подзадачи работает идеально. И я не буду скрывать, любую задачу на ДП можно решить в таких терминах. Но ваша эффективность сильно повысится, если вы научитесь и другому подходу, который я назову симуляцией процесса. Так что это значит?

Подход с симуляцией процесса

Этот подход в основном используется в задачах, где вас просят либо "посчитать число объектов такого вида" или "найти лучший объект такого вида". Идея в том, чтобы придумать некий пошаговый процесс, который строит такой объект. Каждый путь процесса (т.е. последовательность шагов) должен соответсвовать одному объекту. Взглянем на пример.

118D - Легионы Цезаря. После формализации задача звучит так:

Посчитайте количество последовательностей из 0-й и 1-ц, где ровно n0 0-й и ровно n1 1-ц, при этом запрещено иметь более k0 0-й подряд или более k1 1-ц подряд.

Задачи на последовательности – наиболее очевидные кандидаты на симуляуию процесса. В таких задачах процессом обычно является просто "Выпишите последовательность слева направо", по одному элементу на каждом шагу. В данном случае есть два возможных шага: выписать 0 или 1 справа от того, что уже написано. Однако, мы должны допускать только корректные последовательности, поэтому некоторые шаги придётся запретить. Для этого мы вводим параметры процесса. Параметры должны:

1. Определять, какие шаги на данный момент позволены.

2. Быть пересчитываемыми после совершения шага.

3. Отсекать валидные конечные состояния от невалидных.

В данном случае есть следующие правила:

1. Не более n0 0-й всего.

2. Не более n1 1-ц всего.

3. Не более k0 0-й подряд.

4. Не более k1 1-ц подряд.

Поэтому нам потребуется знать следующие параметры процесса:

1. Сколько уже выписано 0-й.

2. Сколько уже выписано 1-ц.

3. Какой последний выписанный символ.

4. Сколько таких символов написано сейчас на конце подряд.

Если мы знаем, чему равны эти параметры, у нас есть вся необходимая информация, чтобы определить, можем ли мы написать ещё один 0 или ещё одну 1, а также пересчитать параметры после того, как совершится один из этих шагов. Когда мы используем этот подход, в массиве dp просто хранится некая информация о всех путях процесса, приводящих в данное состояние (где под состоянием я также имею в виду набор значений для каждого параметра). Если мы хотим сосчитать количество способов выполнить процесс, эта информация будет просто количеством подобных путей. Если мы хотим найти "наилучший" способ совершить процесс, мы храним некую информацию о наилучшем пути среди всех, что приводят в данное состояние, например, его цену или последний шаг на таком пути, если мы хотим позже восстановить ответ.

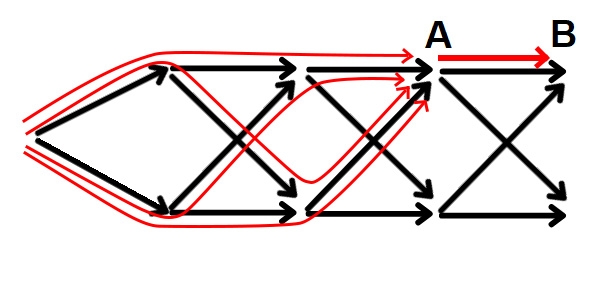
И вот главный трюк: каждый переход в графе ДП – это шаг процесса при некотором состоянии. Когда мы реализуем переход из состояния A в состояние B, мы просто должны обработать все ново-найденные пути, полученные продлением всех путей, ведущих в A, шагом, ведущим их в B. Это не все пути, заканчивающиеся в B, но идея в том, что вы должны обнаружить их всех к моменту, когда начнёте реализовать переходы из B. Если в dp хранится число таких путей, то реализовать переход – означает просто прибавить dp[A] к dp[B], то есть прибавить все ново-найденные пути, попадающие в B через A, к общему количеству путей, кончающихся в B.

Реализация

Если вы когда либо слышали о ДП с переходами вперёд и ДП с переходами назад, вы могли начать подозревать, что эта классификация – и есть та, что я здесь описываю. Однако, я считаю, что классификация переходы вперёд и переходы назад относится лишь реализации. Реализация с переходами назад – это: "Зафиксируем состояние, которое ещё не было посчитано, реалзиуем все переходы, ведущие в него"; тогда как с переходами вперёд – это: "Зафиксируем состояние, что уже было посчитано, реализуем все переходы, исходящие из него".

На самом деле, после того, как вы определились с графом ДП, не важно в каком порядке вы реализуете переходы. Вы можете даже придумать свой способ, если следуете простому правилу: не реализуйте переход из состояния A раньше перехода в состояние A. Но всё же подход с переходами вперёд намного более применим и осмысленен для симуляции процесса, а переходы назад – для обычного ДП, так что эти классификации в 90% случаев совпадают.

Давайте вернёмся к нашей задаче и реализуем решение. Для этого надо определить стартовое состояние процесса. Обозначим за dp[i][j][t][k] состояние, где уже i 0-й, j 1-ц, последний символ – t, и он написан k раз подряд на конце. Очевидно, мы начинаем при i = 0 и j = 0, но чему равны t и k? Строго говоря, если мы начинаем с пустой последовательности, "последнего символа" не существует. Но давайте слегка поменяем описание процесса и скажем, что когда мы начинаем, последним символом считается 0, но он был выписан 0 раз подряд. Так что начальное состояние – dp[0][0][0][0], и начать мы можем только одним способом, так что dp[0][0][0][0] должно быть равно 1.

Остальное довольно просто и интуитивно:

#include <bits/stdc++.h>
#define int int64_t
 
using namespace std;
 
int mod = 1e8;
int dp[101][101][2][11];
 
int32_t main() {
    ios_base::sync_with_stdio(0);
    int n0, n1, k0, k1;
    cin >> n0 >> n1 >> k0 >> k1;
    dp[0][0][0][0] = 1;
    for (int i = 0; i <= n0; i++) {         // переберём все состояния
        for (int j = 0; j <= n1; j++) {     // начиная со стартового
            for (int t = 0; t < 2; t++) {   // в топологическом порядке
                int k = t == 0 ? k0 : k1;
                for (int l = 0; l <= k; l++) {
                    // фиксируем состояние dp[i][j][t][k]
                    if (i < n0 && (t == 1 || l < k)) { // можем ли мы выписать ещё один 0?
                        // если да, то окажемся в этом состоянии
                        (dp[i + 1][j][0][t == 1 ? 1 : l + 1] += dp[i][j][t][l]) %= mod;
                    }
                    if (j < n1 && (t == 0 || l < k)) { // можем ли мы выписать ещё одну 1?
                        // если да, то окажемся в этом состоянии
                        (dp[i][j + 1][1][t == 0 ? 1 : l + 1] += dp[i][j][t][l]) %= mod;
                    }
                }
            }
        }
    }
    int ans = 0;
    for (int t = 0; t < 2; t++) {
        int k = t == 0 ? k0 : k1;
        for (int l = 0; l <= k; l++) {
            // фиксируем одно из корректных финальных состояний процесса
            (ans += dp[n0][n1][t][l]) %= mod;
        }
    }
    cout << ans << endl;
}

Очевидно, временная сложность будет равна количество переходов в графе ДП. В данном случае это O(n0 * n1 * (k0 + k1)).

Ещё один пример

543A - Пишем код Есть n программистов, они должны написать m строк кода сделав не более b ошибок. i-й программист совершает a[i] ошибок за строку. Сколько есть способов это сделать? (Два способа различаются, если различается количество строк, написанных одним из программистов).

Давайте определим процесс, который строит такой объект (корректное распределение m строк кода между n программистами). В условии задачи этот объект был представлен, как последовательность чисел v[1], v[2], ..., v[n] (где v[i] – число строк, написанное i-м программистом), как будто они намекают нам, что это очередная задача на построение последовательности. Давайте попробуем определить шаг процесса, как "написать очередной элемент последовательности", слева направа.

Чтобы последовательность получилась корректной, должны выполняться эти правила:

1. Длина последовательности – n.

2. Сумма элементов равна m.

3. Сумма a[i] * v[i] по всем элементам не превосходит b.

Значит, нам нужны следующие параметры:

1. Количество уже выписанных элементов (количество зафиксированных программистов).

2. Сумма уже выписанных элементов (количество написанных строк кода).

3. Сумма a[i] * v[i] для всех уже выписанных элементов (количество совершённых ошибок).

Число состояний такого процесса будет в районе n * m * b. Но из каждого состояния в среднем будет порядка m / 2 переходов, а именно: "выписать 0", "выписать 1", "выписать 2", ..., "выписать m - s (где s – это текущая сумма)". Так что общее число переходов будет O(n * m^2 * b), что не пройдёт ограничение по времени. Это учит нас тому, что не всегда стоит использовать процесс, описанный в условии, надо мыслить шире.

Давайте придумаем другой процесс. Возможно, вместо того, чтоб идти по программистам, надо идти по строкам? Давайте для каждой строки определим, какой программист её напишет. Чтобы не посчитать одно и то же распределение дважды, скажем, что первый программист пишет первые v[1] строк, второй пишет v[2] следующих строк, и т. д. Так что если строку написал i-й программист, следующую строку могут написать лишь i-й, i + 1-й, ..., n-й. Тогда нам потребуются следующие параметры:

1. Сколько уже написано строк.

2. Какой программист написал последнюю строку.

3. Сколько уже сделано ошибок.

И снова та же проблема: есть около n * m * b состояний и в среднем порядка n / 2 переходов из каждого состояния, а именно: "следующую строку пишет программист i", "следующую строку пишет программист i + 1", ..., "следующую строку пишет программист n". Так что временная сложность будет O(n^2 * m * b), что опять слишком долго.

Если подумать какое-то время, то станет очевидно, что нам в любом случае потребуются эти три параметра: что-то про число программистов, что-то про число строк и что-то про число ошибок. Так что если мы хотим пройти ограничение по времени, нам необходимо сократить количество переходов из каждого состояния, сделать его O(1). Нам явно требуется как минимум два перехода: один будет увеличивать параметр строк, другой будет увеличивать параметр программистов. Если мы подумаем над этим, то получим такой процесс: "В начале за столом сидит программист 1. На каждом шаге либо текущий программист пишет одну строку кода, либо текущий программист уходит, а вместо него за стол садится следующий". Параметры:

1. Какой программист сейчас за столом.

2. Сколько уже написано строк.

3. Сколько уже сделано ошибок.

Начальное состояние: первый программист сидит за столом, написано 0 строк, сделано 0 ошибок. Число переходов – наконец, O(n * m * b). Чтобы сократить потребление памяти, я использую мнимый параметр (это означает, что я храню dp только для текущего значения первого параметра, забывая предыдущие слои). Реализация:

#include "bits/stdc++.h"
 
#define int int64_t

using namespace std;

int mod;

void add(int& a, int b) { // вместо (a += b) %= mod
    a += b;
    if (a >= mod) {
        a -= mod;
    }
}

int32_t main() {
    ios_base::sync_with_stdio(0);
    int n, m, b;
    cin >> n >> m >> b >> mod;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    vector<vector<int>> dp(m + 1, vector<int>(b + 1)); // текущий слой (изначально 0)
    dp[0][0] = 1;
    for (int i = 0; i < n; i++) {
        vector<vector<int>> new_dp(m + 1, vector<int>(b + 1)); // следующий слой (i + 1)
        for (int j = 0; j <= m; j++) {
            for (int k = 0; k <= b; k++) {
                // фиксируем состояние dp(i)[j][k], где i мнимое
                if (i < n - 1) { // есть ли следующий программист?
                    // если есть, посадим его за стол, окажемся в таком состоянии
                    add(new_dp[j][k], dp[j][k]);
                }
                if (j < m && k + a[i] <= b) { // может ли текущий программист написать строчку?
                    // если может, окажемся в данном состоянии
                    add(dp[j + 1][k + a[i]], dp[j][k]);
                }
            }
        }
        if (i < n - 1) {
            dp = new_dp; // перейти к слою i + 1
        }
        
    }
    int ans = 0;
    for (int k = 0; k <= b; k++) {
        // фиксируем одно из корректных финальных состояний процесса
        // (последний программист сидит за столом, все строки написаны)
        add(ans, dp[m][k]);
    }
    cout << ans << endl;
}

Рюкзак

AtCoder DP Contest: Задача D Есть n объектов, i-й имеет вес w[i] и цену v[i]. Какая максимальная сумма цен по всем наборам объектов с суммой весов не более m?

Шаг процесса – это просто: "Посмотрим на следующий объект и либо пропустим его, либо возьмём". Параметры:

1. Сколько объектов мы уже рассмотрели.

2. Сумма весов взятых объектов.

Первый параметр снова будет мнимым, так что мы храним лишь один слой таблицы dp, соответствующий зафиксированному значению первого параметра. Значение dp – максимальная сумма цен взятых объектов по всем путям процесса, ведущим в данное состояние. Реализация:

#include <bits/stdc++.h>

using namespace std;

#define int int64_t

void relax(int& a, int b) {
    a = max(a, b);
}

int32_t main() {
    ios_base::sync_with_stdio(0);
    int n, m;
    cin >> n >> m;
    vector<int> w(n), v(n);
    for (int i = 0; i < n; i++) {
        cin >> w[i] >> v[i];
    }
    vector<int> dp(m + 1, -2e18); // если в состояние не ведёт ни один путь, максимальной ценой считается -inf
    dp[0] = 0;
    for (int i = 0; i < n; i++) {
        vector<int> new_dp = dp; // автоматически реализуем все переходы первого вида
        for (int j = 0; j <= m - w[i]; j++) {
            // фиксируем состояние dp(i)[j], где i мнимое
            relax(new_dp[j + w[i]], dp[j] + v[i]); // переход второго вида
        }
        dp = new_dp; // переходим от слоя i к i + 1
    }
    int ans = -2e18;
    for (int i = 0; i <= m; i++) {
        relax(ans, dp[i]); // фиксируем сумму весов
    }
    cout << ans << endl;
}

Заключение

Есть множество примеров, где этот подход значительно упрощает поиск решения, но я не могу привести все. Если понравился пост, нажмите пожалуйста лайк :)

Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – 1800 руб/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.