I'm glad to invite to take part in USACO contest is from JAN 10 to 13. This contest is IOI style and please don't discuss the problems here before the contest ends! USACO.org
→ Pay attention
→ Streams
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/20/2024 19:44:35 (j1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










How to solve problem "Ski Course Rating" (Gold) ?!
Lets have DSU where for each set we also remember number of cells in it and number of start sites in it. Then we just join pairs of adjacent cells in order of difference between their values. Each time we join some set that had less then T cells and resulting set no less then T cells we add current difference multiplied by number of starting sites to answer
Problem 1: code
We can see that the captured stones are exactly those in the convex hull of the opponent's stones: the stones outside the hull are obviously outside of any triangle, and we can triangulate the opponent's hull into triangles (even disjoint, if we wanted) formed by its vertices.
It's a classic problem of constructing a convex hull and couting points in a convex polygon. Just sort the points of each set by (x-coordinate, in case of equality y-coordinate), and maintain the convex hull of points below the line between the first and last point (with this sorting; inclusive), and the concave hull of points above it; the union of those 2 polylines gives the whole convex hull.
For counting points of the other set in the hull: we have them sorted identically, so we can move a sweepline by increasing x; from a property of convex polygons, we know that if a given point P lies inside the polygon, there's exactly 1 side of the bottom polyline and exactly 1 side of the top polyline which have x-coordinates of its vertices x1, x2 such that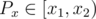 (except Px equal to the maximum x-coordinate of the points of the hull, which can be checked easily). As x increases, the indices of those 2 lines don't decrease, so we can use 2 pointers for identifying them. Checking the "above" and "below" (not strictly) can be done simply using vector cross products.
(except Px equal to the maximum x-coordinate of the points of the hull, which can be checked easily). As x increases, the indices of those 2 lines don't decrease, so we can use 2 pointers for identifying them. Checking the "above" and "below" (not strictly) can be done simply using vector cross products.
Complexity: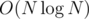 , due to sorting. My code uses closed intervals [x1, x2] and doesn't worry about errors by 1 :D
, due to sorting. My code uses closed intervals [x1, x2] and doesn't worry about errors by 1 :D
Problem 2: code
Let's fix B. Consider this simple bruteforce: we traverse the field and if there's a square BxB with all characters equal, let's mark all the cells of that square as "can contain anything". That's because if we ignore the condition for the resulting snow types in that square, and are able to satisfy them for the rest of the field, we can surely satisfy all of them together, by stamping the selected square BxB last. We repeat the process, where all cells with "whatever" type are considered as both "S" and "R", always stamping squares of all "S" or all "R" (with at least one cell not "whatever"), and if we can stamp the whole field this way, we win.
The generalization to any B is simple: we start with maximum B, repeat the said algorithm, and if we can't stamp anything and a cell is left unstamped, we'll just decrease B (up to B = 1, when it always works).
This is too slow, so let's try for at least O(N2M2); the first obvious improvement is in prefix sums (using which we can count "whatever"s, "R"s and "S"s in any rectangle), which make checking whether to mark the cells of a square as "whatever" simpler. We'll need to update them when marking a cell as "whatever" (so also as either "R" or "S"), but that's simple: for cell (i, j), we just need to increment the prefix sums at cells (k ≥ i, l ≥ j). If we could ensure that this happens for any cell just once, the total time for prefix sum updates is amortized O(N2M2) (O(NM) per cell).
Next, we can store the set S of top left corners of squares which weren't marked with "whatever"s yet; since B is non-increasing, we see that we can ignore the squares with top left corners not in S. That's one more optimization; the set<> operations only take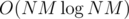 additional operations.
additional operations.
We can now try all squares BxB witn top left corners in S; if none of them are marked "whatever", we can decrease B and repeat; that's done at most O(min(N, M)) times and only takes O(NM) time per pass. If we mark a square with "whatever"s, we can check all its cells and mark all those which haven't been marked yet. We process each top left corner at most once and the square has at most O(NM) cells; the updates of prefix sums have been counted separately, so this takes O(N2M2) time at most.
Now, this complexity is crazy, so I'll pose a mini challenge: find a test case where my code is really slow! :D
Problem 3: code
Consider a graph whose vertices are cells of the grid and there's an edge of cost |di - dj| between cells i, j.
We can sort the edges and use a union-find data structure to store components. Let's add the edges by non-decreasing cost; when adding an edge between 2 different components, we merge the smaller one into the larger one; if the resulting component contains at least T vertices, and at least one of the original ones contains < T vertices, we set the rating of all vertices in that original component (for both original components, if both satisfy the condition) equal to the cost of the added edge.
We can see that each component has vertices with all ratings set or all not yet set, and so we only set the rating of each vertex once.
In the end, we sum up the results for the vertices for which it's required. Complexity: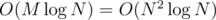 .
.
Well, Egor ninja'd me :D
How to solve the 2nd problem of gold division?
see above
Well, I had a O(NM min(N+M) log min(N + M)) solution
We fix B by having binary search on it (it is obvious that if we can do for some value of B, we can do for all smaller values as well just by applying bigger stamp through series of smaller)
Now let's for each horizontal strip of length B store how much S, R and wildcard pieces are there. Then for each BxB square we need to store how much horizontal strips contain only wildcard and smooth cells, how much contain only wildcard and rough cells and how much contain both smooth and rough and how much are totally wildcard. We than process strip, square and cell state changes, where strip can change state twice (both rough and smooth present, only rough and wildcards or only smooth and wildcards, wildcard only), and cell and square can change state only once (cell from some fixed value to wildcard, square from containing both smooth and rough to being all wildcard). Each of this changes can be processed in O(B), and there are O(NM) total objects
Hi.
Can someone tell me how to solve the Silver problems?
I thought they were simpler than usual USACO contests ( and it's making me feel worried :p ). I tried brute force for the first problem, Binary search for the second and DP for the third one.
I'd love to here from others how they solved those problems.
I don't remember what were the two first problems (I think my solutions were good), but for the third, I submitted a greedy algorithm:
I sorted the differents intervals by increasing end, and, for each interval, if one or more recorders can recorder it, I choose the one who finished to record his last program lastly.
Is there a reason why this algorithm can't work?
Edit: it was a correct greedy: http://pastebin.com/VvCaYRAE
First one was about cow with decreasing speed, looks like it was only about carefully implementing it.
Second one was about finding the minimum absolute difference between two cells which would allow you to reach all the special cells. I see two solutions here. First is binary search over the answer, second one is somehow similar to Djikstra's algorithm on finding the shortest path to every cell. The idea is that you start at some special cell and at every iteration you take in the cell with minimum diff to it. As soon as you took in all the special cells the result would be the maximum weight of the edges you took.
Can't see any so far. I came up with a DP solution but it should run in time. (or so I hope) Here are the three statement to help you recall the ideas.
Bessie Slows Down
Cross Country Skiing
Recording the Moolympics
Edit: The solution I posted was incorrect because it might have considered the same program more than once.
I have a greedy solution for the third problem, though I don't know if it's correct.
Sort the programs by end time and then do the following algorithm...
1) Make both recorders available at time 0. Make ans = 0.
2) At each iteration, find the first program that can be recorded and make the recorder which becomes available last record it. By first, I mean the first in our sorted list, which is, among all the programs that start after some recorder becomes available, the one that ends first. Mark the program as recorded, update the recorder data and make ans = ans+1.
3) End the algorithm when no more programs can be recorded.
You can't record more than 150 programs, and at each iteration you make at most 150 checks, so the overall complexity is O(N2), the problem is I don't know if it's correct.
That's exactly my greedy algorithm :D For the second, I had Dijkstra version.
Edit: Oh wait, it isn't the same. Mine is O(NlogN) (for sorting)
Same algorithm I came up with too.
Results published. I'm gold now :)
Same here :)
wow... not expecting a perfect score on gold (my second problem theoretically should be slow but it run really fast! :D), what a really good day :)
A curious thing: I just tried a very simple heuristic solution to the problem "Building a Ski Course" and I got 9/10 test cases OK.
The solution is as follows...
1) For every row, find the maximum number of equal adjacent elements.
2) Do the same for every column.
3) Find the maximum square size so that all elements inside it are equal.
4) Output the minimum among all those numbers.
I don't think USACO bothers with test cases too much, seeing as there so few of them. My solution on Curling got WA 2 times, so it should've gotten WA much more often, too — yet it didn't. Your approach is a reasonable approximation, so it's no wonder that it works often — large random cases, for example, give the results 2 or 3 almost always.
A lot of people have WA on "curling" problem's last test case, where both teams have their stones placed along a line. I think it's reasonable to assume that triangle means non-degenerated triangle, isn't it?
I assumed that the authors didn't assume it, and accounted for it when thinking. Even so, I failed because I forgot to code the special case of points on a vertical line...
Yes, triangle usually means exactly a triangle. But USACO usually doesn't follow logic. You can write to the organizers if you want.