Нет, я не имею в виду Convex Hull-оптимизацию и оптимизацию Кнута. Я имею в виду более простые и распространённые методы.

Это продолжение моей серии постов о ДП, чтобы понимать обозначения, читайте пролог.

Переходы из отрезка

Очень часто после построения графа динамики можно обнаружить, что переходы в то или иное состояние ведут не из случайного набора вершин, а из некоторого отрезка по одному из параметров. Например, из состояний dp[i][j], при некотором константном i и при j, лежащим в отрезке [a, b].

В таком случае можно не реализовывать каждый переход в отдельности, а реализовать все скопом. Если под реализацией перехода понимается прибавление из dp[A] в dp[B], то можно воспользоваться префиксной суммой. Если же нам нужно найти наилучший переход в dp[B], то можно воспользоваться деревом отрезков.

Пример

AtCoder DP Contest: Задача M Найти количество целочисленных последовательностей длины n, где i-е число от 0 до a[i], а сумма чисел равна k.

Решим методом симуляции процесса. Рассмотрим процесс выписывания по одному числу последовательности. Параметрами процесса будут:

1. Сколько мы уже выписали чисел.

2. Сумма выписанных чисел.

Значением динамики dp[i][j] будет количество путей процесса, ведущих в данное состояние.

Количество переходов из одного состояния равно O(k), общее количество переходов – O(n k^2), слишком долго.

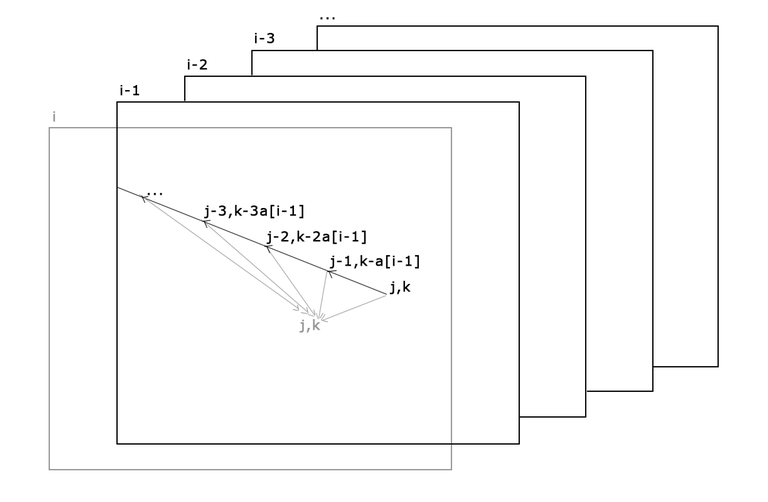
Рассмотрим, откуда ведут переходы в состояние dp[i][j]. Очевидно, из dp[i - 1][l], где l принадлежит отрезку [max(0, j - a[i - 1]), j].

Значит, перед тем, как считать слой i, можно насчитать префиксные суммы на слое i - 1, чтобы считать dp[i][j] за O(1).

#include <bits/stdc++.h>

#define int int64_t

using namespace std;

int mod = 1e9 + 7;

int32_t main() {
    ios_base::sync_with_stdio(false);
    int n, k;
    cin >> n >> k;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    vector<int> dp(k + 1); // текущий слой (мнимый параметр)
    dp[0] = 1;
    for (int i = 0; i < n; i++) {
        vector<int> sum(dp.size() + 1); // префикс-суммы текущего слоя
        for (int j = 0; j < dp.size(); j++) {
            sum[j + 1] = sum[j] + dp[j];
        }
        vector<int> new_dp(k + 1); // следующий слой
        for (int j = 0; j <= k; j++) {
            new_dp[j] = (sum[j + 1] - sum[max(int64_t(0), j - a[i])]) % mod;
        }
        dp = new_dp;
    }
    cout << dp[k] << endl;
}

Переходы из косого отрезка

Вернёмся к задаче из прошлой части моего блога.

543A - Пишем код Есть n программистов, они должны написать m строк кода, сделав не более b ошибок. i-й программист совершает a[i] ошибок за строку. Сколько есть способов это сделать? (Два способа различаются, если различается количество строк, написанных одним из программистов).

Вспомним самое первое решение: определим процесс, где за один шаг мы назначаем очередному программисту количество написанных им строк. Параметрами будут:

1. Количество пройденных программистов.

2. Суммарное количество написанных строк.

3. Суммарное количество сделанных ошибок.

Значением динамики dp[i][j][k] будет количество путей процесса, ведущих в данное состояние.

Тогда состояний всего получается O(n m b), а переходов из одного состояния – O(m), значит всего переходов – O(n m^2 b), что слишком много.

Но давайте рассмотрим, из каких состояний есть переход в состояние dp[i][j][k]. Если последний шаг был "i - 1-й программист написал x строк кода", то переход был из состояния dp[i - 1][j - x][k - x * a[i - 1]] (где x >= 0).

То есть состояния, из которых ведёт переход, расположены на некоторой прямой в таблице i - 1-ого слоя, и в общем случае сумму всех таких значений можно за O(1) вычислить из аналогичной суммы для состояния dp[i][j - 1][k - a[i - 1]].

После некоторых упрощений код выглядит так:

#include <bits/stdc++.h>

using namespace std;

#define int int64_t

int mod;

void add(int& a, int b) { // вместо (a += b) %= mod
    a += b;
    if (a >= mod) {
        a -= mod;
    }
}

int32_t main() {
    ios_base::sync_with_stdio(0);
    int n, m, b;
    cin >> n >> m >> b >> mod;
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
    }
    vector<vector<int>> dp(m + 1, vector<int>(b + 1)); // текущий слой
    dp[0][0] = 1;
    for (int i = 0; i < n; i++) { // переход от слоя i к i + 1
        for (int j = 0; j < m; j++) {
            for (int k = 0; k <= b - a[i]; k++) {
                add(dp[j + 1][k + a[i]], dp[j][k]);
            }
        }
    }
    int ans = 0;
    for (int k = 0; k <= b; k++) {
        add(ans, dp[m][k]);
    }
    cout << ans << endl;
}

Поменять местами значение и параметр

Эта техника стара, как мир. Если один из параметров слишком большой, а значение наоборот ограничено, можно попробовать поменять их ролями.

Пример

AtCoder DP Contest: Задача E Есть n объектов, i-й имеет вес w[i] и цену v[i]. Какая максимальная сумма цен по всем наборам объектов с суммой весов не более m? В этой версии задачи n <= 100, m <= 10^9, v[i] <= 10^3.

Возьмём решение из предыдущей части блога: рассмотрим процесс, где на каждом шагу рассматривается очередной объект и либо выбирается, либо пропускается, параметрами процесса будут:

1. Количество рассмотренных объектов.

2. Суммарный вес выбранных объектов.

Значением динамики будет наибольшая сумма стоимостей выбранных объектов при данном состоянии процесса.

При данных ограничениях, максимальное значение второго параметра будет 10^9, а максимальное значение динамики – 10^5, поэтому имеет смысл поменять их ролями. Процесс будет тем же самым, но параметрами будут:

1. Количество рассмотренных объектов.

2. Суммарная стоимость выбранных объектов.

Значением динамики будет наименьшая сумма весов выбранных объектов при данном состоянии процесса.

В конце мы рассмотрим наибольшую сумму стоимостей объектов из числа тех, для которых минимальный суммарный вес не больше W.

#include <bits/stdc++.h>

using namespace std;

#define int int64_t

void relax(int& a, int b) {
    a = min(a, b);
}

const int max_v = 1e5;

int32_t main() {
    ios_base::sync_with_stdio(0);
    int n, m;
    cin >> n >> m;
    vector<int> w(n), v(n);
    for (int i = 0; i < n; i++) {
        cin >> w[i] >> v[i];
    }
    vector<int> dp(max_v + 1, 2e18); // если в состояние не ведёт ни один путь, минимальной суммой считается inf
    dp[0] = 0;
    for (int i = 0; i < n; i++) {
        vector<int> new_dp = dp; // автоматически реализуем все переходы первого вида
        for (int j = 0; j <= max_v - v[i]; j++) {
            // фиксируем состояние dp(i)[j], где i мнимое
            relax(new_dp[j + v[i]], dp[j] + w[i]); // переход второго вида
        }
        dp = new_dp; // переходим от слоя i к i + 1
    }
    int ans = 0;
    for (int i = 0; i <= max_v; i++) {
        if (dp[i] <= m) {
            ans = i;
        }
    }
    cout << ans << endl;
}

Объединить два параметра

Иногда мы можем заметить о неких параметрах, что нам необязательно знать значение каждого, а достаточно следить за некой их комбинацией. Например, если в конце мы делаем проверку на то, что сумма двух параметров не должна превышать некоторое значение, то возможно у нас получится заменить эти два параметра на один, равный их сумме.

Пример

19B - Кассир Есть n товаров, у каждого есть цена c[i] и время обработки t[i]. Найдите множество товаров с минимальной суммарной ценой такое, что их суммарное время обработки не меньше количества остальных товаров.

Рассмотрим процесс, где на каждом шагу рассматривается очередной товар и либо выбирается, либо пропускается. Параметрами процесса будут:

1. Количество рассмотренных товаров.

2. Суммарное время обработки выбранных товаров.

3. Количество невыбранных товаров.

Значением динамики будет минимальная суммарная стоимость выбранных товаров при данном состоянии процесса.

По итогу нас интересуют состояния dp[n][j][k], где j >= k. Так как k <= n, мы будем считать, что если параметр j достиг n, то в дальнейшем нет смысла его повышать, так что все состояния процесса при больших значениях параметра j будем записывать, будто j = n.

Таким образом количество состояний равно O(n^3), как и количество переходов, что не проходит под ограничения.

Рассмотрим подробнее, куда ведут переходы из состояния dp[i][j][k]: в случае выбора товара – в dp[i + 1][j + t[i]][k], а в случае пропуска – в dp[i + 1][j][k + 1].

Заметим, что в первом случае разность второго и третьего параметров просто увеличивается на t[i], во втором случае – уменьшается на 1, а в конце нужно отсечь те состояния, где эта разность неотрицательна, следовательно вместо каждого этого параметра по отдельности, можно следить за их разностью.

Для удобства вместо j - k будем следить за j + i - k (чтобы параметр был неотрицательным, т. к. k <= i), тогда при выборе товара параметр увеличивается на t[i] + 1, а при пропуске не изменяется.

Так как в конце отсекаются состояния, где этот параметр не меньше n, при этом он ни при каком переходе не уменьшается, то можно аналогично предыдущему решению записывать состояния с j + i - k > n в dp[i][n].

Таким образом, количество состояний и переходов оба равны O(n^2).

#include <bits/stdc++.h>

using namespace std;

#define int int64_t

void relax(int& a, int b) {
    a = min(a, b);
}

int32_t main() {
    ios_base::sync_with_stdio(0);
    int n;
    cin >> n;
    vector<int> t(n), c(n);
    for (int i = 0; i < n; i++) {
        cin >> t[i] >> c[i];
    }
    vector<int> dp(n + 1, 2e18); // текущий слой (мнимый параметр)
    dp[0] = 0;
    for (int i = 0; i < n; i++) {
        vector<int> new_dp = dp; // применяем переходы второго вида
        for (int j = 0; j <= n; j++) {
            relax(new_dp[min(n, j + t[i] + 1)], dp[j] + c[i]);
        }
        dp = new_dp; // переходим к следующему слою
    }
    cout << dp[n];
}

Заключение

Если хотите узнать больше, я напоминаю, что даю частные уроки по спортивному программированию, цена – 1800 руб/ч. Пишите мне в Telegram, Discord: rembocoder#3782, или в личные сообщения на CF.