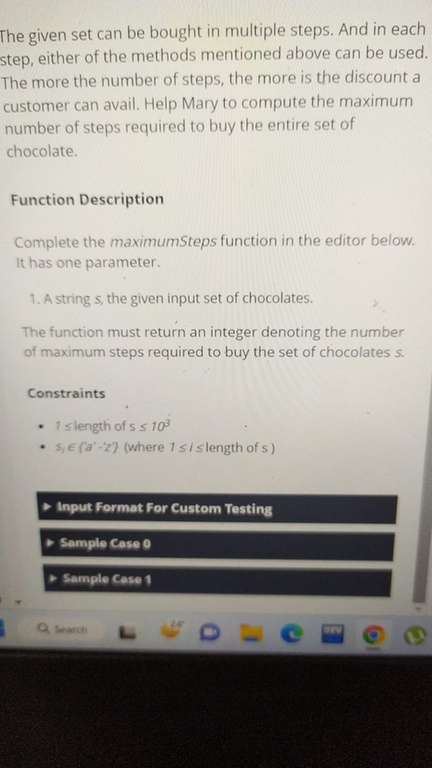
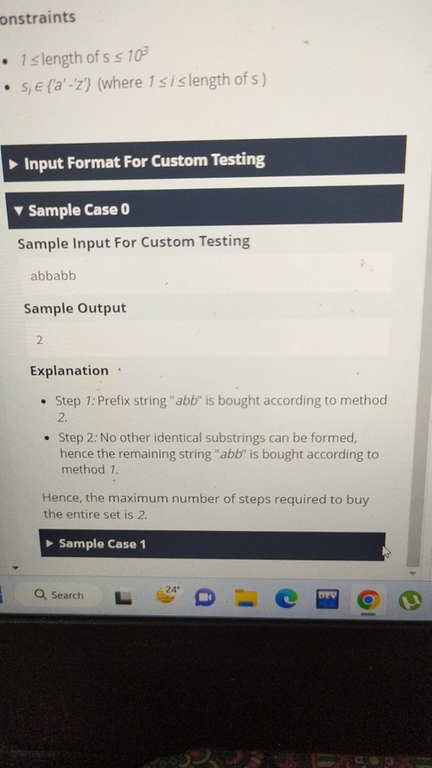
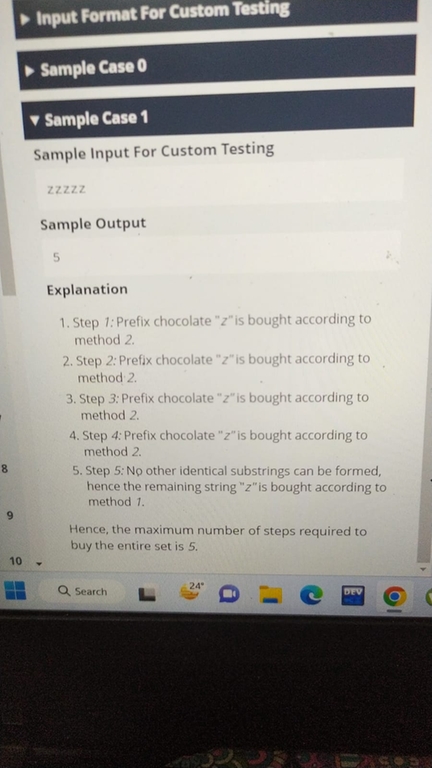
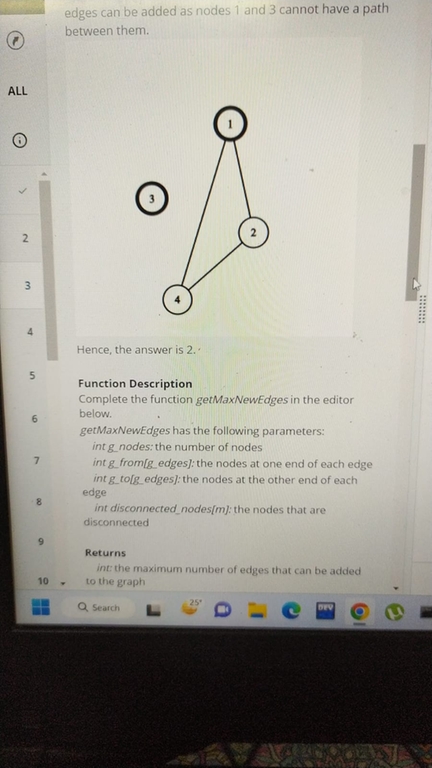
I got 3 questions. First was medium but doable. I was not able to solve question 2 and 3. Can someone help me out with the solution Question 2:

Question 3:

| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | jiangly | 3977 |
| 2 | tourist | 3815 |
| 3 | jqdai0815 | 3682 |
| 4 | ksun48 | 3614 |
| 5 | orzdevinwang | 3526 |
| 6 | ecnerwala | 3514 |
| 7 | Benq | 3483 |
| 8 | hos.lyric | 3381 |
| 9 | gamegame | 3374 |
| 10 | heuristica | 3358 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | -is-this-fft- | 162 |
| 3 | Um_nik | 161 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 157 |
| 5 | Dominater069 | 157 |
| 7 | adamant | 154 |
| 8 | luogu_official | 152 |
| 8 | awoo | 152 |
| 10 | TheScrasse | 148 |
I got 3 questions. First was medium but doable. I was not able to solve question 2 and 3. Can someone help me out with the solution Question 2:




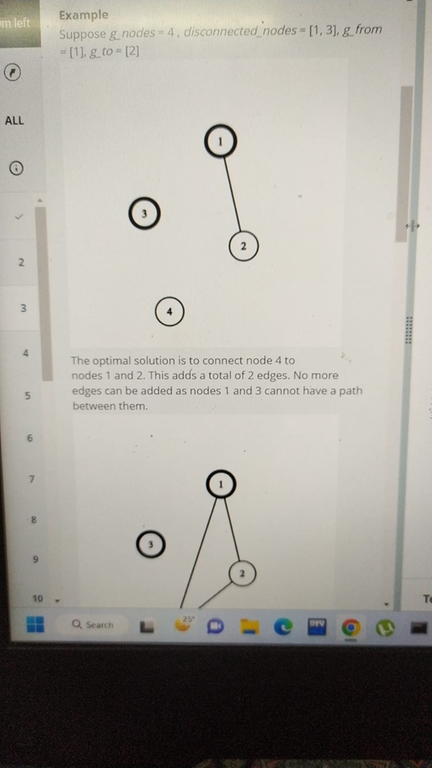
Question 3:







| Название |
|---|



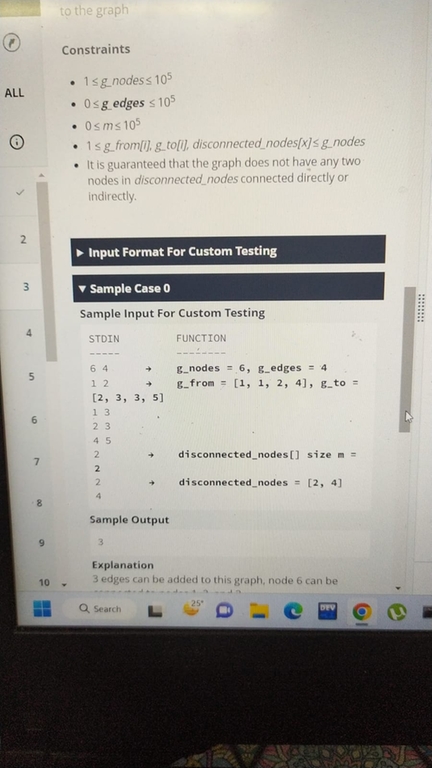
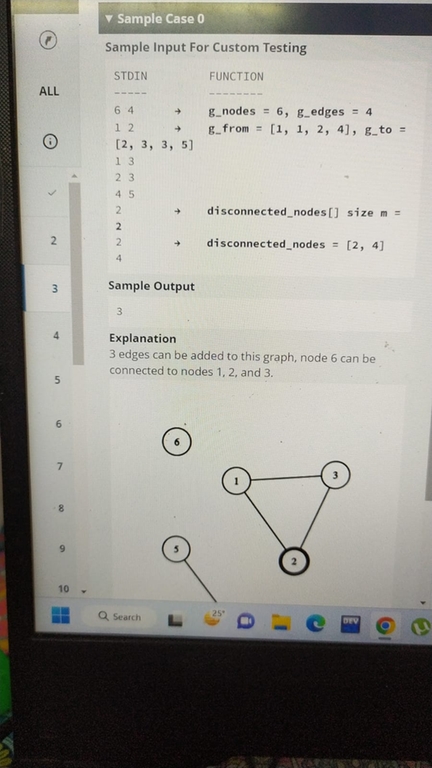
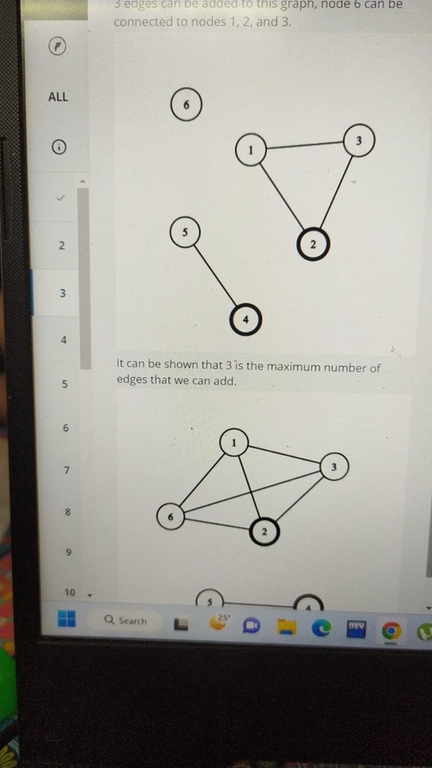
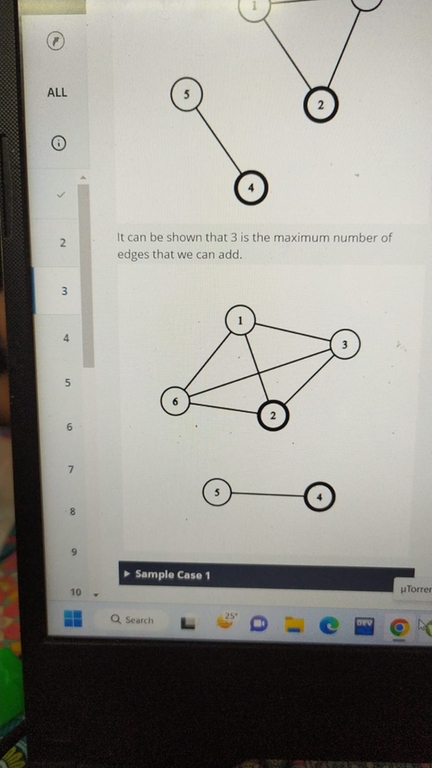
For Q3 first use dsu to get disconnected components of graph. We can add additional edges in each component without issue. Now check the disconnected components which do not contain any disconnected_nodes. We can add edges among them without issue and lets call this new component as R. Last, choose the biggest component with a disconnected_node and we can add edges among the nodes of that component and R. Max Number of edges in a component of size n is nC2. Get maximum number of edges and subtract current number of edges to get answer For Q2, we can use repeated z-algorithm along with dp.
so connect all components which do not have node a disconnected node. Now take the largest components which has a disconnected component . And now connect both these components
Yes. But we also have to add additional edges in each connected component which already has a disconnected_node.
i think in Q2 this greedy solution won't work...hence i did it with dp
Can you please share the logic
Can you tell your approach for the 1st problem?
If you multiply any integer by 2 you are just right shifting the bits and you want msb as right as possible so its optimal to do all the operation for one integer only, check for all the integer in O(1) and return the maximum
Q3