Hello
I need help in this problem which is kind of famous
Given N numbers N<=10^5 and Q Queries Q<=10^5 of the type:
Modify X , Y modify the Xth number into Y
Count X , Y count how many distinct integers are between the Xth number and the Yth number (inclusive)
actually i have seen this problem (or problems similiar) a lot on the internet
i searched but i didn't find any answer
so can you help me please??!!
I've just come up with an
offline solution using a two-dimensional compressed segment tree. Let's notice, on what segments the answer will change if we modify the number at the Xth position. So, it's pretty easy to understand that the answer will decrease by 1 on all segments that cover position X and contain only one instance of Yold. In the same way, the answer will increase by 1 on all segments that cover position X and don't contain any instances of Ynew. So, to quickly perform a query of the first type, you need to be able to perform addition on a rectangle. I mean: you need to make a 2D segment tree, where coordinate X will mean the left end of a 2nd type query's segment and coordinate Y — the right one. This tree will need O(n2) memory, so you need to compress it, storing only those points that are found among the 2nd type queries. A detailed explanation of such a tree can be found here (article is in Russian, use Google Translate).
P.S. I'm very sorry for a not very detailed explanation, so please think hard while reading it.
Actually i know what are segment trees ... but can you explain more? actually i see that your solution is impossible to implement in the complexity you said
But do you know about two-dimensional segment trees and the way to compress them?
In the literatur this is called a range tree, in case somebody wants to do further research. It should actually be able to support orthogonal range queries/updates in
as well
I can think of a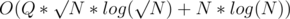
algorithm using square root decomposition and std: : map. Let me know if you want me to elaborate.
Yeah, that was my idea... but it's kind of slow. And you can use Fenwick trees instead, which improves the performance.
Yes! Feeling good that I thought similar to Xellos! :P
On a more serious note, Fenwick trees instead of what?
Instad of maps, of course. The constant factor is much smaller in that case.
yes please ... i think your solution is simpler than the written above
Can't it be solved in O(n*sqrt(n))?sqrt(10^5)=317 and (log^2 n) = 289. But 2D segment tree could be slow because of recursion. Also sqrt segmentation code can be simpler,smaller and easy to code.
I think there must be O(nlog^2n) online solution. You should look into self-balancing trees.
I mean if we build a segment tree and store in each node matching items it will take O(NlogN) memory. And if we represent those elements with any self-balanced tree which can merge in O(logN) (Treaps) or in O(1) (Splay trees), it will become easy to merge all elements into one big tree and count the number of elements in it.
P.S. It's just a guess. Maybe I wrote nonsense.
and modification -_-
AFAIK, it's generally impossible to merge sets in less than Ω(n). So, your solution will be Ω(n2) :).
this editorial explain solution to that problem using 1D segment tree, to be honest, I didn't understand at all (already) but I think code is well explained, I hope could be useful for you: https://www.hackerrank.com/blog/101feb14-coloring-tree
To be honest, it seems that you didn't try to read the editorial carefully.
In fact, you didn't even read this post carefully, because the problem in the editorial is much easier: you don't need to modify array elements in it.
In fact, that particular problem is even easier than the problem the solution explained in the editorial is intended for. In the "Coloring Tree" problem all possible query segments are either non-intersecting or nested, so it can be solved just by set merging in either
or 
. The idea is to DFS the tree and to maintain a set of colors for each vertex. It's obvious that to get a set of colors for a particular vertex, you need to merge sets of colors of its children and add its own color to the merged set. It can be done in 
set operations totally (the idea is to merge sets by adding elements of the smaller one to the larger one).
When I read this post I remember that problem but I was thinking about queries and updates, I didn't read problem again (I read it more than two weeks ago), before posting I'll read information carefully instead on be confident on my memory.
Sorry.