Statement
Given $$$n$$$ strings. Find the string $$$s$$$ with minimum length such that each of $$$n$$$ given strings is a substring of $$$s$$$.
Constraint
$$$n \le 50$$$
Every of $$$n$$$ strings has length not exceed $$$10$$$
Example:
Input:
3
ab
ba
abb
Output:
abba
This problem is hard for me. Can you give me a hint? Thank you in advance.
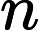
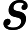
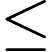
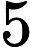
Is it similar to this question?
https://mirror.codeforces.com/gym/104049/problem/K
Because depending on the constraints it can get really hard really fast
I have successfully solved the easy version of it but hard version, I can't
You can see that n = 10, so that's the hint that you're able to test every combination. However how to test every combination? A quick way is with string hashing
look to comment pavook
Your solution is incorrect. Consider the test:
Your program returns the string
abcaxabcxb, while a considerably shorter stringaxabcxbcontains all the substrings, too.yes, you are right. I modified the code and used SCS. thx
Your solution is still incorrect, though it performs a bit better on trivial tests. Consider the test:
Your solution returns the string
aaacaeceee, while the stringaaaecaeeeis shorter, but also contains all the substrings.If you look at my other comment, you'll understand, that designing an exact polynomial algorithm for this problem is in principle very hard.
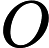
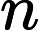
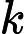
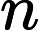
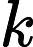
This problem is known as the "Shortest common superstring" problem and is NP-hard (see Wikipedia ). This means solving it in $$$O(n^k)$$$ where $$$n$$$ is the summary length of strings, and $$$k$$$ is any fixed number, would be a major breakthrough in Computer Science.
Moreso, we can't even provably 2-approximate the answer (create an answer with length not greater than double the minimum possible).
You'll probably achieve best results using some approximate methods, e.g. simulated annealing.
Thank you
Can't it be done by creating a suffix automaton?
We can do something sort of topological sorting on the trie having suffix links(or failure links) and then start creating the final string which we need using dfs?
That wouldn't always be an optimal solution. Indeed, there's a conjecture that a variation of the algorithm you suggested 2-approximates the solution.
By the way, trie with suffix links is basically Aho-Corasick automaton. And it makes sense that it's possible to construct a solution with such a structure: think about it -- the Aho-Corasick algorithm basically checks character-by-character, that all the substrings are present in our string.
Thank You.
By the way, if possible, please provide pseudo code for the approximation methods like simulated annealing. I am new on this,so It would be a great help.
One of the problems similar to this :Fullmetal Alchemist II
Auto comment: topic has been updated by I_need_7.0_IELTS (previous revision, new revision, compare).
Auto comment: topic has been updated by I_need_7.0_IELTS (previous revision, new revision, compare).
I think it's a NP-hard problem? So it's impossible to give an answer in polynomial time. You cant solve it in time using a O(K^n) algorithm :)