I was using the Berlekamp-Massey (BM) algo for yesterday's H, but my sol worked too slow. Here is my idea:
(1) Divide [1,n] into scales. Let S(scale) be the scale scale, which is S(scale) is {x|x×scale≥n,x×scale/2<n}. For example, if n=7, scale 1 is [7,7], scale 2 is [4,6], scale 4 is [2,3], scale 8 is [1,1]. It is guaranteed that scale is a power of 2 in my sol.
(2)Fetch O(logscale) consecutive items for each scale using the matrix fast power algorithm. The matrix is constructed in step (3) from the last scale.
(3)Using the BM algorithm to build a recurrence of length O(logscale) and a recurrence matrix M∈Z/pZO(logscale)×O(logscale).
I mean for each scale we fetch some items I, get a recurrence using the BM algorithm, and construct a recurrence matrix M using that recurrence, for example ar=ar+1+ar+2, then
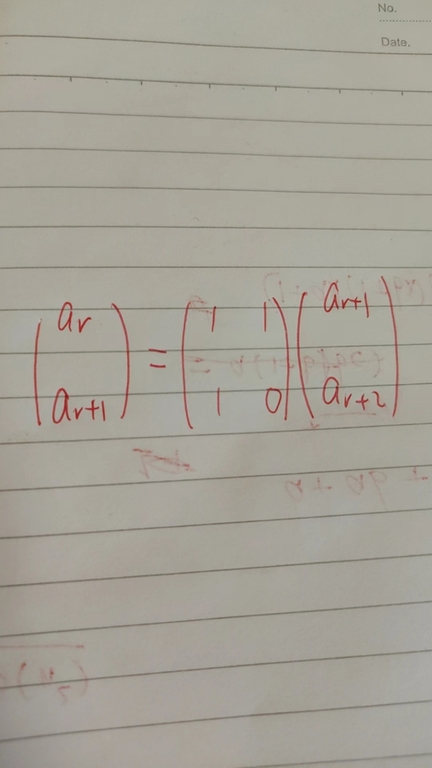
The matrix M and the items I, and the fast matrix power algorithm, are used to fetching items for the next scale. This is a coarse-to-fine algorithm. The problem is that, for each scale, I need to fetch O(logscale) items and each item costs O(logscale3logn) using a fast matrix power algorithm (matrix multiplication is O(logscale3), and there are up to O(n) elements for each scale. Therefore the complexity for each scale is O(logscale4logn) and the overall complexity is ∑scaleO(logscale4logn)=O((logn)6) for each test case which is too slow. Any idea to speed up?
Code:
#define ATCODER 0
#include <bits/stdc++.h>
#if ATCODER
#include <atcoder/all>
using namespace atcoder;
#endif
using namespace std;
#pragma GCC optimize("Ofast,unroll-loops")
#pragma GCC target("avx2,tune=native")
#define ull unsigned long long
#define lp (p << 1)
#define rp ((p << 1)|1)
#define ll long long
#define ld long double
#define pb push_back
#define all(s) s.begin(), s.end()
#define sz(x) (int)(x).size()
#define fastio cin.tie(0) -> sync_with_stdio(0)
#define pii pair<int, int>
#define pil pair<int, ll>
#define pli pair<ll, int>
#define pll pair<ll, ll>
#define F(i, a, b) for(int i=(a); i <= (b); ++i)
#define SUM 0
#define MAX 1
#define fi first
#define se second
#define il inline
#define YES cout << "YES\n"
#define Yes cout << "Yes\n"
#define NO cout << "NO\n"
#define No cout << "No\n"
#define cans cout << ans << "\n"
#define PQ(TYPE, FUNCTOR) priority_queue<TYPE, vector<TYPE>, FUNCTOR<TYPE>>
#define HERE printf("HERE, __LINE__==%d\n", __LINE__);
#define INF 0x3f3f3f3f
#define INFLL 0x3f3f3f3f3f3f3f3fll
#define ld long double
#define fl std::cout << setprecision(15) << fixed
#define BT(x, i) (((x) & (1 << (i))) >> (i))
#define BTLL(x, i) (((x) & (1ll << (i))) >> (i))
const ld pi = acosl(-1);
long long power(long long a, long long b, int mod)
{
long long res=1;
while(b>0)
{
//a=a%mod;(有时候n的值太大了会超出long long的储存,所以要先取余)
if(b&1)//&位运算:判断二进制最后一位是0还是1,&的运算规则为前后都是1的时候才是1;
res=res*a%mod;
b=b>>1;//相当于除以2;
a=a*a%mod;
}
return res;
}
template<typename T, T...>
struct myinteger_sequence { };
template<typename T, typename S1 = void, typename S2 = void>
struct helper{
std::string operator()(const T& s){
return std::string(s);
}
};
template<typename T>
struct helper<T, decltype((void)std::to_string(std::declval<T>())), typename std::enable_if<!std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::to_string(s);
}
};
template<typename T>
struct helper<T, void, typename std::enable_if<std::is_same<typename std::decay<T>::type, char>::value, void>::type>{
std::string operator()(const T& s){
return std::string(1, s);
}
};
template<typename T, typename S1 =void, typename S2 =void>
struct seqhelper{
const static bool seq = false;
};
template<typename T>
struct seqhelper<T, decltype((void)(std::declval<T>().begin())), decltype((void)(std::declval<T>().end()))>{
const static bool seq = !(std::is_same<typename std::decay<T>::type, std::string>::value);
};
template<std::size_t N, std::size_t... I>
struct gen_indices : gen_indices<(N - 1), (N - 1), I...> { };
template<std::size_t... I>
struct gen_indices<0, I...> : myinteger_sequence<std::size_t, I...> { };
template<typename T, typename REDUNDANT = void>
struct converter{
template<typename H>
std::string& to_string_impl(std::string& s, H&& h)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h));
return s;
}
template<typename H, typename... T1>
std::string& to_string_impl(std::string& s, H&& h, T1&&... t)
{
using std::to_string;
s += converter<H>().convert(std::forward<H>(h)) + ", ";
return to_string_impl(s, std::forward<T1>(t)...);
}
template<typename... T1, std::size_t... I>
std::string mystring(const std::tuple<T1...>& tup, myinteger_sequence<std::size_t, I...>)
{
std::string result;
int ctx[] = { (to_string_impl(result, std::get<I>(tup)...), 0), 0 };
(void)ctx;
return result;
}
template<typename... S>
std::string mystring(const std::tuple<S...>& tup)
{
return mystring(tup, gen_indices<sizeof...(S)>{});
}
template<typename S=T>
std::string convert(const S& x){
return helper<S>()(x);
}
template<typename... S>
std::string convert(const std::tuple<S...>& tup){
std::string res = std::move(mystring(tup));
res = "{" + res + "}";
return res;
}
template<typename S1, typename S2>
std::string convert(const std::pair<S1, S2>& x){
return "{" + converter<S1>().convert(x.first) + ", " + converter<S2>().convert(x.second) + "}";
}
};
template<typename T>
struct converter<T, typename std::enable_if<seqhelper<T>::seq, void>::type>{
template<typename S=T>
std::string convert(const S& x){
int len = 0;
std::string ans = "{";
for(auto it = x.begin(); it != x.end(); ++it){
ans += std::move(converter<typename S::value_type>().convert(*it)) + ", ";
++len;
}
if(len == 0) return "{[EMPTY]}";
ans.pop_back(), ans.pop_back();
return ans + "}";
}
};
template<typename T>
std::string luangao(const T& x){
return converter<T>().convert(x);
}
static std::random_device rd; // random device engine, usually based on /dev/random on UNIX-like systems
// initialize Mersennes' twister using rd to generate the seed
static std::mt19937_64 rng{rd()};
//jiangly Codeforces
int P = 998244353;
using i64 = long long;
// assume -P <= x < 2P
int norm(int x) {
if (x < 0) {
x += P;
}
if (x >= P) {
x -= P;
}
return x;
}
template<class T>
T power(T a, i64 b) {
T res = 1;
for (; b; b /= 2, a *= a) {
if (b % 2) {
res *= a;
}
}
return res;
}
struct Z {
int x;
Z(int x = 0) : x(norm(x)) {}
Z(i64 x) : x(norm((int)(x % P))) {}
int val() const {
return x;
}
Z operator-() const {
return Z(norm(P - x));
}
Z inv() const {
assert(x != 0);
return power(*this, P - 2);
}
Z &operator*=(const Z &rhs) {
x = i64(x) * rhs.x % P;
return *this;
}
Z &operator+=(const Z &rhs) {
x = norm(x + rhs.x);
return *this;
}
Z &operator-=(const Z &rhs) {
x = norm(x - rhs.x);
return *this;
}
Z &operator/=(const Z &rhs) {
return *this *= rhs.inv();
}
friend Z operator*(const Z &lhs, const Z &rhs) {
Z res = lhs;
res *= rhs;
return res;
}
friend Z operator+(const Z &lhs, const Z &rhs) {
Z res = lhs;
res += rhs;
return res;
}
friend Z operator-(const Z &lhs, const Z &rhs) {
Z res = lhs;
res -= rhs;
return res;
}
friend Z operator/(const Z &lhs, const Z &rhs) {
Z res = lhs;
res /= rhs;
return res;
}
friend std::istream &operator>>(std::istream &is, Z &a) {
i64 v;
is >> v;
a = Z(v);
return is;
}
friend std::ostream &operator<<(std::ostream &os, const Z &a) {
return os << a.val();
}
};
template<typename T>
T exgcd(T &x, T &y, T a, T b)
{
if(!b)
{
x=1;
y=0;
return a;
}
exgcd(x,y,b,a%b);
T t=x;
x=y;
y=t-a/b*y;
return x*a+y*b;
}
#define MAXN 200005
// stores smallest prime factor for every number
int spf[MAXN];
bool notprime[MAXN];
int prime[MAXN], miu[MAXN], ptot;
int phi[MAXN];
// Calculating SPF (Smallest Prime Factor) for every
// number till MAXN.
// Time Complexity : O(nloglogn)
void sieve()
{
spf[1] = 1;
for (int i=2; i<MAXN; i++)
// marking smallest prime factor for every
// number to be itself.
spf[i] = i;
// separately marking spf for every even
// number as 2
for (int i=4; i<MAXN; i+=2)
spf[i] = 2;
for (int i=3; i*i<MAXN; i++)
{
// checking if i is prime
if (spf[i] == i)
{
// marking SPF for all numbers divisible by i
for (int j=i*i; j<MAXN; j+=i)
// marking spf[j] if it is not
// previously marked
if (spf[j]==j)
spf[j] = i;
}
}
}
void getmiu()
{
memset(notprime, 0, sizeof(notprime));
miu[1] = 1;
ptot = 0;
miu[1] = 1;
for(int i = 2; i < MAXN; i++) {
if(!notprime[i]) {
prime[ptot++] = i;
miu[i] = -1;
}
for(int j = 0; j < ptot && prime[j] * i < MAXN; j++) {
int k = prime[j] * i;
notprime[k] = true;
if(i % prime[j] == 0) {
miu[k] = 0; break;
} else {
miu[k] = -miu[i];
}
}
}
}
void getphi()
{
int n = MAXN - 1;
for (int i = 1; i <= n; i++)
phi[i] = i; // 除1外没有数的欧拉函数是本身,所以如果phi[i] = i则说明未被筛到
for (int i = 2; i <= n; i++)
if (phi[i] == i) // 未被筛到
for (int j = i; j <= n; j += i) // 所有含有该因子的数都进行一次操作
phi[j] = phi[j] / i * (i - 1);
}
template<typename T>
void facsieve(T x, map<T, T>& f)
{
while (x != 1)
{
f[spf[x]]++;
x = x / spf[x];
}
}
template<typename T>
void facnaive(T x, map<T, T>& f){
for (T p = 2; p * p <= x; ++p) {
if (x % p == 0) {
T k = 1;
for (x /= p; x % p == 0; x /= p) ++k;
f[p]+=k;
}
}
if (x > 1) f[x]++;
}
ll intsqrt (ll x) {
ll ans = 0;
for (ll k = 1LL << 30; k != 0; k /= 2) {
if ((ans + k) * (ans + k) <= x) {
ans += k;
}
}
return ans;
}
ll safelog(ll x){
for(ll i = 63; i >= 0; --i){
if(BTLL(x, i)) return i;
}
return -1;
}
template<typename T>
struct perf{
uint64_t t1, t2;
std::string hintline="";
bool verbose;
bool is_run;
perf():verbose(true), is_run(true){
t1 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
}
perf(std::string hintline):hintline(hintline), verbose(true), is_run(true){
t1 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
}
~perf(){
if(!is_run) return;
t2 = (uint64_t)std::chrono::time_point_cast<T>(std::chrono::system_clock::now()).time_since_epoch().count();
if(verbose)
std::cout << hintline << ": current:" << t2 - t1 << "\n";
is_run = false;
}
};
using perfm = perf<std::chrono::microseconds>;
template<typename S>
struct shash{
const S& t;
int radix, base;
std::vector<int> primes;
constexpr std::pair<long long, long long> inv_gcd(long long a, long long b) {
a = safe_mod(a, b);
if (a == 0) return {b, 0};
// Contracts:
// [1] s - m0 * a = 0 (mod b)
// [2] t - m1 * a = 0 (mod b)
// [3] s * |m1| + t * |m0| <= b
long long s = b, t = a;
long long m0 = 0, m1 = 1;
while (t) {
long long u = s / t;
s -= t * u;
m0 -= m1 * u; // |m1 * u| <= |m1| * s <= b
// [3]:
// (s - t * u) * |m1| + t * |m0 - m1 * u|
// <= s * |m1| - t * u * |m1| + t * (|m0| + |m1| * u)
// = s * |m1| + t * |m0| <= b
auto tmp = s;
s = t;
t = tmp;
tmp = m0;
m0 = m1;
m1 = tmp;
}
// by [3]: |m0| <= b/g
// by g != b: |m0| < b/g
if (m0 < 0) m0 += b / s;
return {s, m0};
}
constexpr long long safe_mod(long long x, long long m) {
x %= m;
if (x < 0) x += m;
return x;
}
struct barrett {
unsigned int _m;
unsigned long long im;
// @param m `1 <= m < 2^31`
barrett(){}
void set(unsigned int m){
_m = m;
im = (unsigned long long)(-1) / m + 1;
}
explicit barrett(unsigned int m) : _m(m), im((unsigned long long)(-1) / m + 1) {}
// @return m
unsigned int umod() const { return _m; }
// @param a `0 <= a < m`
// @param b `0 <= b < m`
// @return `a * b % m`
unsigned int mul(unsigned int a, unsigned int b) const {
// [1] m = 1
// a = b = im = 0, so okay
// [2] m >= 2
// im = ceil(2^64 / m)
// -> im * m = 2^64 + r (0 <= r < m)
// let z = a*b = c*m + d (0 <= c, d < m)
// a*b * im = (c*m + d) * im = c*(im*m) + d*im = c*2^64 + c*r + d*im
// c*r + d*im < m * m + m * im < m * m + 2^64 + m <= 2^64 + m * (m + 1) < 2^64 * 2
// ((ab * im) >> 64) == c or c + 1
unsigned long long z = a;
z *= b;
#ifdef _MSC_VER
unsigned long long x;
_umul128(z, im, &x);
#else
unsigned long long x =
(unsigned long long)(((unsigned __int128)(z)*im) >> 64);
#endif
unsigned int v = (unsigned int)(z - x * _m);
if (_m <= v) v += _m;
return v;
}
};
struct dynamic_modint {
using mint = dynamic_modint;
int mod() { return (int)(bt.umod()); }
static mint raw(int v) {
mint x;
x._v = v;
return x;
}
dynamic_modint() : _v(0) {}
template<typename T>
dynamic_modint(T v, int m) {
bt.set(m);
long long x = (long long)(v % (long long)(mod()));
if (x < 0) x += mod();
_v = (unsigned int)(x);
}
unsigned int val() const { return _v; }
mint& operator++() {
_v++;
if (_v == umod()) _v = 0;
return *this;
}
mint& operator--() {
if (_v == 0) _v = umod();
_v--;
return *this;
}
mint operator++(int) {
mint result = *this;
++*this;
return result;
}
mint operator--(int) {
mint result = *this;
--*this;
return result;
}
mint& operator+=(const mint& rhs) {
_v += rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator-=(const mint& rhs) {
_v += mod() - rhs._v;
if (_v >= umod()) _v -= umod();
return *this;
}
mint& operator*=(const mint& rhs) {
_v = bt.mul(_v, rhs._v);
return *this;
}
mint& operator/=(const mint& rhs) { return *this = *this * rhs.inv(); }
mint operator+() const { return *this; }
mint operator-() const { return mint() - *this; }
mint pow(long long n) const {
assert(0 <= n);
mint x = *this, r = 1;
while (n) {
if (n & 1) r *= x;
x *= x;
n >>= 1;
}
return r;
}
mint inv() const {
auto eg = inv_gcd(_v, mod());
assert(eg.first == 1);
return eg.second;
}
friend mint operator+(const mint& lhs, const mint& rhs) {
return mint(lhs) += rhs;
}
friend mint operator-(const mint& lhs, const mint& rhs) {
return mint(lhs) -= rhs;
}
friend mint operator*(const mint& lhs, const mint& rhs) {
return mint(lhs) *= rhs;
}
friend mint operator/(const mint& lhs, const mint& rhs) {
return mint(lhs) /= rhs;
}
friend bool operator==(const mint& lhs, const mint& rhs) {
return lhs._v == rhs._v;
}
friend bool operator!=(const mint& lhs, const mint& rhs) {
return lhs._v != rhs._v;
}
private:
unsigned int _v;
barrett bt;
unsigned int umod() { return bt.umod(); }
};
std::map<int, std::vector<dynamic_modint>> f; //不同素数的前缀和
std::map<int, std::vector<dynamic_modint>> radixmap;
shash()=delete;
shash(const S& t, int radix=27, int base=(int)'a'-1, std::vector<int> primes={998244353, 1000000007}):t(t), radix(radix), base(base), primes(primes){
for(int p: primes){
f[p].resize(t.size());
radixmap[p].resize(t.size());
f[p][0] = dynamic_modint(0, p);
dynamic_modint tmp(radix, p);
radixmap[p][0] = dynamic_modint(1, p);
for(int i = 1; i < t.size(); ++i){
f[p][i] = f[p][i-1]*tmp + dynamic_modint(t[i] - base, p);
radixmap[p][i] = radixmap[p][i-1] * tmp;
}
}
}
std::map<int, dynamic_modint> operator()(const int l, const int r){
std::map<int, dynamic_modint> res;
if(l > r) return res;
for(int p: primes){
res[p] = f[p][r] - f[p][l-1]*radixmap[p][r-l+1];
}
return res;
}
std::map<int, dynamic_modint> operator()(){
return this->operator()(1, (int)t.size()-1);
}
std::map<int, dynamic_modint> operator()(const std::vector<std::pair<int, int>>& prs){
std::map<int, dynamic_modint> res;
for(int p: primes){
res[p] = dynamic_modint(0, p);
}
for(const auto& [l, r]: prs){
std::map<int, dynamic_modint> res2 = this->operator()(l, r);
if(res2.empty()){
continue;
}else{
for(int p: primes){
res[p] = res[p]*radixmap[p][r-l+1] + res2[p];
}
}
}
return res;
}
};
struct dsu{
int n;
int *pa, *dsusz;
dsu(int n): n(n){
pa = new int[n+1];
dsusz = new int[n+1];
reset();
}
int find(int x){
if(pa[x] == x) return x;
pa[x] = find(pa[x]);
return pa[x];
}
int un(int x, int y, int swapsz=1){
int fx = find(x), fy = find(y);
if(fx == fy) return -1;
if(dsusz[fx] > dsusz[fy] && swapsz) swap(fx, fy);
pa[fx] = fy;
dsusz[fy] += dsusz[fx];
dsusz[fx] = 0;
return fy;
}
int comp(){
int st = 0;
for(int i = 1; i <= n; ++i){
if(pa[i] == i){
++st;
}
}
return st;
}
void reset(){
for(int i = 1; i <= n; ++i){
pa[i] = i;
dsusz[i] = 1;
}
}
~dsu(){
delete[] pa;
delete[] dsusz;
}
};
template<typename T=int, typename S=T>
struct BIT{
bool usep;
int n, digits;
T* p; //元素类型
S* q; //数组类型
template<typename SIGNED>
SIGNED lowbit(SIGNED x){
return x & (-x);
}
BIT(int n, T* p=nullptr):n(n), digits(0), p(p){
usep = (p != nullptr);
q = new S[n+1];
memset(q, 0, (n+1)*sizeof(S));
getdigits();
if(usep) init();
}
void init(){
//O(n)时间内建树
for(int i = 1; i <= n; ++i){
q[i] += (S)p[i];
int j = i + lowbit(i);
if(j <= n) {
q[j] += q[i];
}
}
}
void add(int x, int k){
while(x <= n && x >= 1){
q[x] = q[x] + (S)k;
x += lowbit(x);
}
}
S getsum(int x){
S ans = 0;
while(x >= 1){
ans += q[x];
x -= lowbit(x);
}
return ans;
}
void getdigits(){
if(digits) return;
int tmp = n;
while(tmp){
tmp >>= 1;
digits++;
}
}
int search(S target){
//最长前缀和
int t = 0;
S s = 0;
for(int i = digits-1; i >= 0; --i){
if((t + (1 << i) <= n) && (s + q[t + (1<<i)] <= target)){
s += q[t + (1<<i)];
t += (1 << i);
}
}
return t;
}
int binsearch(S target){
int l = 1, r = n, ans = 0;
while(l <= r){
int mid = (l + r)/2;
if(getsum(mid) == target){
ans = mid;
l = mid + 1;
}else if(getsum(mid) < target){
l = mid + 1;
}else{
r = mid - 1;
}
}
return ans;
}
~BIT(){
delete[] q;
}
};
vector<int> digits(ll x){
stack<int> st;
while(x){
st.push(x%10);
x/=10;
}
vector<int> res;
while(!st.empty()){
res.push_back(st.top());
st.pop();
}
return res;
}
bool isprime(int x){
if(x <= 3) return (x!=1);
for(int i = 2; i * i <= x; ++i){
if(x%i == 0){
return false;
}
}
return true;
}
struct Comb {
int n;
std::vector<Z> _fac;
std::vector<Z> _invfac;
std::vector<Z> _inv;
Comb() : n{0}, _fac{1}, _invfac{1}, _inv{0} {}
Comb(int n) : Comb() {
init(n);
}
void init(int m) {
if (m <= n) return;
_fac.resize(m + 1);
_invfac.resize(m + 1);
_inv.resize(m + 1);
for (int i = n + 1; i <= m; i++) {
_fac[i] = _fac[i - 1] * i;
}
_invfac[m] = _fac[m].inv();
for (int i = m; i > n; i--) {
_invfac[i - 1] = _invfac[i] * i;
_inv[i] = _invfac[i] * _fac[i - 1];
}
n = m;
}
Z fac(int m) {
if (m > n) init(2 * m);
return _fac[m];
}
Z invfac(int m) {
if (m > n) init(2 * m);
return _invfac[m];
}
Z inv(int m) {
if (m > n) init(2 * m);
return _inv[m];
}
Z binom(int n, int m) {
if (n < m || m < 0) return 0;
return fac(n) * invfac(m) * invfac(n - m);
}
} comb;
namespace atcoder {
namespace internal {
template <class E> struct csr {
std::vector<int> start;
std::vector<E> elist;
explicit csr(int n, const std::vector<std::pair<int, E>>& edges)
: start(n + 1), elist(edges.size()) {
for (auto e : edges) {
start[e.first + 1]++;
}
for (int i = 1; i <= n; i++) {
start[i] += start[i - 1];
}
auto counter = start;
for (auto e : edges) {
elist[counter[e.first]++] = e.second;
}
}
};
// Reference:
// R. Tarjan,
// Depth-First Search and Linear Graph Algorithms
struct scc_graph {
public:
explicit scc_graph(int n) : _n(n) {}
int num_vertices() { return _n; }
void add_edge(int from, int to) { edges.push_back({from, {to}}); }
// @return pair of (# of scc, scc id)
std::pair<int, std::vector<int>> scc_ids() {
auto g = csr<edge>(_n, edges);
int now_ord = 0, group_num = 0;
std::vector<int> visited, low(_n), ord(_n, -1), ids(_n);
visited.reserve(_n);
auto dfs = [&](auto self, int v) -> void {
low[v] = ord[v] = now_ord++;
visited.push_back(v);
for (int i = g.start[v]; i < g.start[v + 1]; i++) {
auto to = g.elist[i].to;
if (ord[to] == -1) {
self(self, to);
low[v] = std::min(low[v], low[to]);
} else {
low[v] = std::min(low[v], ord[to]);
}
}
if (low[v] == ord[v]) {
while (true) {
int u = visited.back();
visited.pop_back();
ord[u] = _n;
ids[u] = group_num;
if (u == v) break;
}
group_num++;
}
};
for (int i = 0; i < _n; i++) {
if (ord[i] == -1) dfs(dfs, i);
}
for (auto& x : ids) {
x = group_num - 1 - x;
}
return {group_num, ids};
}
std::vector<std::vector<int>> scc() {
auto ids = scc_ids();
int group_num = ids.first;
std::vector<int> counts(group_num);
for (auto x : ids.second) counts[x]++;
std::vector<std::vector<int>> groups(ids.first);
for (int i = 0; i < group_num; i++) {
groups[i].reserve(counts[i]);
}
for (int i = 0; i < _n; i++) {
groups[ids.second[i]].push_back(i);
}
return groups;
}
private:
int _n;
struct edge {
int to;
};
std::vector<std::pair<int, edge>> edges;
};
} // namespace internal
struct scc_graph {
public:
scc_graph() : internal(0) {}
explicit scc_graph(int n) : internal(n) {}
void add_edge(int from, int to) {
int n = internal.num_vertices();
assert(0 <= from && from < n);
assert(0 <= to && to < n);
internal.add_edge(from, to);
}
std::vector<std::vector<int>> scc() { return internal.scc(); }
private:
internal::scc_graph internal;
};
} // namespace atcoder
#define DEBUG 1
#define SINGLE 0
#define cstr(x) (luangao(x).c_str())
void debug(const char* p){
#if DEBUG
freopen(p, "r", stdin);
#else
fastio;
#endif
}
constexpr int p = 998244353;
#define cstr(x) (luangao(x).c_str())
vector<int> berlekamp_massey(vector<int> a, int p) {
for(int& x: a){
if(x < 0) x%=p, x+=p;
}
vector<int> v, last; // v is the answer, 0-based, p is the module
int k = -1, delta = 0;
for (int i = 0; i < (int)a.size(); i++) {
int tmp = 0;
for (int j = 0; j < (int)v.size(); j++)
tmp = (tmp + (long long)a[i - j - 1] * v[j]) % p;
if (a[i] == tmp) continue;
if (k < 0) {
k = i;
delta = (a[i] - tmp + p) % p;
v = vector<int>(i + 1);
continue;
}
vector<int> u = v;
int val = (long long)(a[i] - tmp + p) * power(delta, p - 2, p) % p;
if (v.size() < last.size() + i - k) v.resize(last.size() + i - k);
(v[i - k - 1] += val) %= p;
for (int j = 0; j < (int)last.size(); j++) {
v[i - k + j] = (v[i - k + j] - (long long)val * last[j]) % p;
if (v[i - k + j] < 0) v[i - k + j] += p;
}
if ((int)u.size() - i < (int)last.size() - k) {
last = u;
k = i;
delta = a[i] - tmp;
if (delta < 0) delta += p;
}
}
for (auto &x : v) x = (p - x) % p;
v.insert(v.begin(), 1);
return v; // $$$\forall i, \sum_{j = 0} ^ m a_{i - j} v_j = 0$$$
}
vector<vector<Z>> getmatrix(vector<int>& bm){
vector<vector<Z>> res;
int m = (int)bm.size()-1;
res.resize(m+1);
F(i, 0, m) res[i].resize(m+1);
F(i, 1, m){
F(j, 1, m){
if(i == 1){
res[i][j] = -Z(bm[j]);
}
else{
res[i][j] = (i - j == 1);
}
}
}
return res;
}
vector<vector<Z>> matmul(vector<vector<Z>>& a, vector<vector<Z>>& b){
int m = a.size()-1;
vector<vector<Z>> res(m+1, vector<Z>(m+1));
F(i, 1, m){
F(j, 1, m){
F(k, 1, m){
res[i][j] += a[i][k] * b[k][j];
}
}
}
return res;
}
vector<vector<Z>> fp(vector<vector<Z>>& bm, ll x){
int m = bm.size()-1;
if(x == 0){
vector<vector<Z>> res(m+1, vector<Z>(m+1));
F(i, 1, m){
F(j, 1, m){
res[i][j] = (i == j);
}
}
return res;
}else if(x == 1) return bm;
auto tmp = fp(bm, x/2);
auto res = matmul(tmp, tmp);
if(x%2){
res = matmul(res, bm);
}
return res;
}
void solve(int test){
ll n;
cin >> n;
ll scale = 1; //处理x * scale >= n的区间
vector<vector<Z>> lastbm;
vector<Z> lastres, lastres2;
auto getlbub = [&](ll scale) -> pll{
return {(n + scale - 1)/scale, (scale == 1 ? n : ((n + scale/2 - 1)/(scale/2) - 1))};
};
function<Z(ll)> getans = [&](ll x) -> Z{
if(x >= n) return 0;
if(scale/2 * x >= n){
//assert(lastres.size()+1 == lastbm.size());
//属于上一个scale
auto [lastlb, lastub] = getlbub(scale/2);
int m = (int)lastbm.size()-1;
ll diff = lastub - x;
if(diff < lastres.size()){
//printf("[1]scale==%lld, x==%lld, diff==%lld, ans==%d, lastres.size()==%zu, lastbm.size()==%zu\n", scale, x, diff, lastres[diff].val(), lastres.size(), \
lastbm.size());
return lastres[diff];
}
ll times = diff - m + 1;
auto fpres = fp(lastbm, times);
//printf("lastres.size()==%zu, m==%d\n", lastres.size(), m);
Z ans = 0;
for(int i = 1; i <= m; ++i){
ans += fpres[1][i] * lastres[m - i];
}
//printf("[2]scale==%lld, x==%lld, ans==%lld\n", scale, x, ans);
return ans;
}
return 1 + getans(x+1)/2 + getans(2*x)/2;
};
ll scaletimes = 0;
while(scale <= n){
auto [lb, ub] = getlbub(scale);
lastres2.clear();
vector<int> trial;
vector<int> lastbmres;
ll x = ub;
for(; x >= max(lb, ub-3*scaletimes); --x){
Z res = getans(x);
trial.pb(res.val());
lastres2.pb(res);
}
lastbmres = berlekamp_massey(trial, P);
//printf("scale==%lld, x==%lld, lastbmres==%d\n", scale, x, (int)lastbmres.size());
printf("scale==%lld[%lld, %lld], trial==%s, lastbmres==%s\n", scale, lb, ub, cstr(trial), cstr(lastbmres));
lastres = lastres2;
lastbm = getmatrix(lastbmres);
scale *= 2;
++scaletimes;
}
Z ans = getans(1);
cans;
}
signed main(int argc, char** argv){
debug(argc==1?"test1.txt":argv[1]);
int t = 1;
int test = 1;
#if !SINGLE
cin >> t;
#endif
while(t--){
solve(test++);
}
}









