Доброго времени суток всем.
Сегодня я хочу рассказать немного о написании элегантной структуру данных — Heavy-light decomposition (далее просто HLD).
Многие из вас, наверное, сталкивались с задачами вида "дано взвешенное дерево, запросы модификации ребер и запросы нахождения минимума на ребрах между двумя вершинами". HLD умеет довольно просто решать эту и многие другие задачи.
Для начала краткое описание структуры.
// Более полное описание есть на e-maxx.
Heavy-light decomposition — это такая разбивка графа на непересекающиеся по вершинам или ребрам пути, что на пути от любой вершины до корня этого дерева мы сменим не более log(N) путей. Если мы научимся строить такие пути, то с помощью дополнительных структур (дерево отрезков (или просто ДО), например) сможем быстро отвечать на запросы.
Назовем ребро тяжелым, если поддерево сына, в которого ведет это ребро, будет по размеру не менее половины поддерева отца. Другими словами, 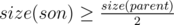 . Заметим, что с вершины вниз может выходить не более одного тяжелого ребра.
. Заметим, что с вершины вниз может выходить не более одного тяжелого ребра.
"И что это нам дает?" — спросите Вы. А дает это нам следующее: если мы возьмем все вершины, из которых не выходит тяжелое ребро, и будем подниматься к корню, пока его не достигнем или не пройдем по легкому ребру, то это и будут нужные нам пути.
Построив дерево отрезков над каждым из путей, мы сможем за log2(N) отвечать на самые разные запросы между двумя вершинами (максимум и т.д.). Нужно будет аккуратно подниматься от вершин к их lca (наименьший общий предок) и производить запросы на ДО или на еще чём-то.
Теперь о количестве кода..
Первый раз, когда я попробовал написать эту структуру для задачи, то код был, мягко говоря, немаленький. Я честно искал lca, честно строил над каждым из путей ДО и еще много чего. Я код еще и дебажил немало. И сейчас стоит поговорить о том, как уменьшить его количество.
О построении HLD
Первое, что хочется исправить, так это немного неудобное построение. Хоть и написать его не составить большинству труда, но мне и сейчас в таком виде, как описано выше, его писать не очень удобно. Вот бы взять, и за один-два простеньких dfs-a это все построить...
И это возможно. Можно строить декомпозицию так: пускай мы находимся в некоторой вершине. Она принадлежит некоторому пути. Рассмотрим всех сынов этой вершины — мы можем продолжить этот путь только в одного, а все остальные сыны станут началом новых путей. В какого же сына надо продолжить этот путь? Правильно, в того, у которого наибольшее поддерево. Значит, один dfs нужен, чтобы подсчитать размеры поддеревьев, а другой для непосредственного построения декомпозиции.
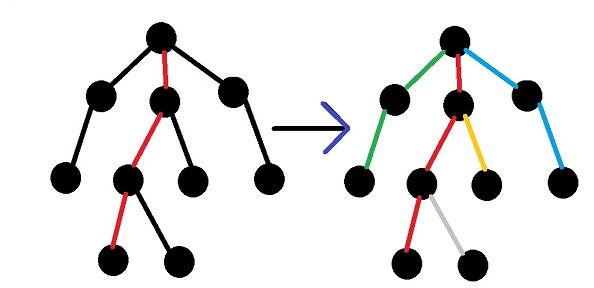
Об отдельных структурах для каждого пути
Далее я буду рассказывать на примере ДО, так как часто именно оно нужно для задач.
Следующая мысль после того, как мы научились просто строить HLD, у меня была приблизительно такая: "Блин, это же надо еще и для каждого пути ДО писать". Да, это не так сложно, но немного было для меня неудобно. Но потом можно понять, что достаточно одного ДО. Необходимо так перенумеровать вершины, чтобы для каждого пути все вершины были на одном подотрезке. Имеем, что нужно только одно ДО.
О честном нахождении lca
Еще одна вещь, через которую разрастался код, — отдельное написание поиска lca. Как же с этим можно бороться?
Оказывается, что не нужно искать lca я явном виде. Давайте поступим по следующему алгоритму: рассмотрим два пути, на которых сейчас наши вершины. Если они на одном пути, то это просто запрос на ДО. А если нет? Тогда давайте выберем путь, у которого наивысшая вершина ниже. Далее просто перейдем в предка этой вершины. Будем так продолжать, пока не придем в один путь. Параллельно всем этим подъемам будем делать запросы на ДО, тем самым ища ответ.
Имеем, что ответ на запрос и нахождение lca можно делать одновременно.
Материалы
Я очень благодарен сайту e-maxx, на котором есть хорошее описание (клац) этой структуры. Я много в чем опирался именно на эту статью.
Еще хорошие материалы есть здесь.
И короткая реализация есть здесь
Бонус
Можно проверить свою HLD на этой задаче. А здесь мой код к ней.
Другие задачи: QTREE, Aladdin and the Return Journey.
P.S. Я понимаю, что простота этой структуры — штука относительная. Я старался объяснить, как мне писать проще. Буду очень рад, если статья кому-то пригодится.
P.P.S Это моя первая статья. Буду рад услышать конструктивную критику, замечания по поводу статьи.











Спасибо за статью.
Можно пример задач, которые нельзя решить никак иначе, и обязательно нужно будет использовать HLD? Обычно получается как-то обойти это и сдать что-нибудь другое.
Ну, сложно сказать, там можно применить совсем разные корневые эвристики, насколько я знаю. Буду рад, если кто предложить решение без ХЛД этой задачи.
Если не трудно, можете дать ссылку на пример кода обхода ХЛД?
Если уж говорить об минимизации количества двсов, то что мешает считать размеры поддеревьев и строит пути в одним? Если не строить для каждого пути до, а хранить все в одном дереве, то асимптотика запроса на пути(например максимума) имеет оценку в log^2, а если бы каждый путь был в своем дереве, суммарно выходило бы log на запрос. Обрадовался увидев название поста, после прочтения слегка разочаровался.
Да, вы правы, спасибо за замечания.
На одном ДО тоже можно достичь logN на запрос, если хранить для каждого пути на всем пути нужную величину (скажем, максимум).
совсем не понимаю, как вы достигаете лог на запрос? вы считаете, что почти все частичные запросы будут покрывать весь путь и его ДО или я не понял тему?
Да, почти все запросы будут "найти функцию на всем пути".
UPD: Бред, можно не читать.
Но это же неверно. Большинство запросов будет на префикс, так как переходя из одного пути в другой, мы попадаем не обязательно в самый низ пути.
К примеру, на Вашей картинке, из желтого или серого пути в красный.
Да, что-то я конкретно ступил, прошу прощения.
Так возможно ли как-то заставить HLD обрабатывать запрос за логарифм или это просто легенды?
я слышал про такое
Вопрос к знатокам HLD: если у нас есть двоичное дерево размера N и мы на пути от каждой вершины до корня делаем запрос, то правда, что суммарно это будет работать за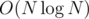 ?
?
Да, и не только в двоичном, а в любом дереве. upd: если писать не так, как автор предлагает, а отдельные до стоить. upd2: или так, как он написал выше в комментарии.
Will you write an English Version ?? If you won't ... I will write one :D ?
у меня вот мое решение на задачу QTREE получает TL. Вот мой код где реализован запрос за log^2N. Знатоки, разъясните пожалуйста на пальцах, как писать за logN. Вот код. Не исключено, что там есть баг, но раньше получал АС где проходила сложность log^2N.
Спасибо большое за статью, советы даны очень полезные. Код вышел вполне читаемым и удобоваримым. Никто, кстати, не подскажет, есть ли на кодфорсах задачи на хеви-лайт? На Споже/Тимусе мне лень что-то отрешивать:)
На емаксе вроде есть две ссылки на задачи с КФа.
Там одна Ешка, которую вообще непонятно как решать:(
В комментариях смотрели? Там еще одна Ешка, только второго дива
(http://blog.anudeep2011.com/heavy-light-decomposition/)
487E - Туристы вот еще задача, на которой можно потренироваться писать HLD.
is it can to solve qtree without hld? for example with centroid decomposition or some other technique?
Back when I saw this problem, I didn't know HLD and I solved it with 2D segment tree. But my solution was way harder than the solution with HLD. :)
Nice Post. I tried to solve this problem but i am getting WA on TC 13. Can anyone help me? My code.
I think your update function is wrong, try to do using a void function, this way your solution pass untill TC 17. To get AC change your lca function, because your lca complexity is O(n) and it's to slow , probably something like this code works.
Thanks for your help
I tried to solve this problem. But it's giving me wrong answer verdict on test case 7. This is my code.
The english version of the e-maxx tutorial can be found here.