Коротко:
Речь пойдет в основном про Heavy-Light decomposition (далее HLD).
Мне интересно, существует ли реализации HLD, допускающие change-запросы и работающие в среднем за 
на get-запрос. Если да, пожалуйста, ссылку в студию. Если нет, докажите (опровергните), пожалуйста, идею кэширования (ниже подробно описана).
Подробно :
1) Введение
HLD или, иначе говоря, покрытие дерева вертикальными путями, позволяет отвечать на различные запросы на дереве... Как дерево отрезков на массиве, только на путях дерева. Почитать про HLD можно на е-maxx.ru.
2) Условие задачи
Я не буду стремиться обобщить свои мысли, а приведу их на примере конкретной задачи: у каждой вершины дерева v есть значение a[v], нужно уметь делать операции a[v] = x, и getMax(a, b) -- найти максимум на пути от a до b. Задачу можно посылать на тимус 1553. Caves and Tunnels (на самом деле Caves and Tunnels проще, т.к. там a[v] всегда только возрастает, но сейчас это не важно...)
3) Возможные решения задачи
Я знаю два способа решать такую задачу: Heavy-Light decomposition и Linking-Cutting trees (почитать можно здесь). HLD за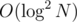 
на запрос. Link-Cut за , если использовать Splay дерево (почитать можно здесь), и за те же 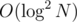, если использовать любое другое дерево, например, декартово.
HLD с точки зрения кодинга мне нравится гораздо больше чем Link-Cut. Решение задачи Caves and Tunnels через HLD весит чуть больше 2K, code. Общий вид LinkCut весит чуть больше 3K code. Из того, что я видел, данные реализации наиболее короткие.
Возникает желание заставить HLD работать так же быстро, как и Linking-Cutting trees со Splay деревом внутри...
4) Оптимизируем HLD
Давайте закэшируем результат внутреннего get-а. Внутренний get, обращающийся к дереву отрезков, всегда (кроме случая в самом верху) считает максимум на префиксе, т.е. запрос зависит только от вершины v. Давайте хранить cash[v] (максимум на префиксе), calcTime[v] (время, когда мы считали этот максимум), и changeTime[tree[v]] (время, когда последний раз менялось соответствующее дерево отрезков), и, если changeTime[tree[v]] < calcTime[v], то не нужно считать еще раз, можно сразу вернуть cash[v].
Теперь время обработки одного запроса = (последний внутренний get) + (количество внутренних get-ов) +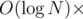 
{количество незакэшированных префиксов}. При этом все ранее незакэшированные префиксы закэшируются.
5) Вопросы
Вопрос #1: а не работает ли это амортизационно за ? (у меня строгого доказательства придумать не получилось).
Вопрос #2: идея, кажется, простая. Но я о ней узнал только сегодня. Кто-нибудь этим пользуется (на контестах, например)? Откуда это известно?
Вопрос #3: вы знаете другие способы заставить HLD работаеть за ?
Вопрос #4: может быть, я туплю, и задача на самом деле решается за на запрос, но проще (без HLD и Link-Cut)?
Конец
Excuse me for commenting in English, but my Russian is not so good.
About question 3: I think the following enhancement to the basic H-L decomposition should work for O(logn): In the H-L decomposition, for each heavy path, we build some kind of accumulative data structure (index, or segment tree), which answers the composition of element of a given interval in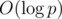
time, where p is the length of the path. A simple enhancement to this is to add to such an index tree an element, which will hold the composition of all of the elements in the interval, making the query O(1) on for the full interval. This just adds an additive constant to the update operation. Now, every (internal node — another descendant internal node) path in the tree is a path containing at most 
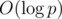light edges and 
heavy paths, but actually only the first and the last of the heavy paths could potentially be not the full heavy paths. For the internal paths, we could use this additional information, to answer the composition of all element along them in O(1). For the cornering heavy paths, we just will have to do at most another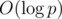 
queries, so the total query time should stay 
. But I may be missing something here...
Actually, not true.