Коротко:
Речь пойдет в основном про Heavy-Light decomposition (далее HLD).
Мне интересно, существует ли реализации HLD, допускающие change-запросы и работающие в среднем за 
на get-запрос. Если да, пожалуйста, ссылку в студию. Если нет, докажите (опровергните), пожалуйста, идею кэширования (ниже подробно описана).
Подробно :
1) Введение
HLD или, иначе говоря, покрытие дерева вертикальными путями, позволяет отвечать на различные запросы на дереве... Как дерево отрезков на массиве, только на путях дерева. Почитать про HLD можно на е-maxx.ru.
2) Условие задачи
Я не буду стремиться обобщить свои мысли, а приведу их на примере конкретной задачи: у каждой вершины дерева v есть значение a[v], нужно уметь делать операции a[v] = x, и getMax(a, b) -- найти максимум на пути от a до b. Задачу можно посылать на тимус 1553. Caves and Tunnels (на самом деле Caves and Tunnels проще, т.к. там a[v] всегда только возрастает, но сейчас это не важно...)
3) Возможные решения задачи
Я знаю два способа решать такую задачу: Heavy-Light decomposition и Linking-Cutting trees (почитать можно здесь). HLD за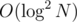 
на запрос. Link-Cut за , если использовать Splay дерево (почитать можно здесь), и за те же 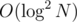, если использовать любое другое дерево, например, декартово.
HLD с точки зрения кодинга мне нравится гораздо больше чем Link-Cut. Решение задачи Caves and Tunnels через HLD весит чуть больше 2K, code. Общий вид LinkCut весит чуть больше 3K code. Из того, что я видел, данные реализации наиболее короткие.
Возникает желание заставить HLD работать так же быстро, как и Linking-Cutting trees со Splay деревом внутри...
4) Оптимизируем HLD
Давайте закэшируем результат внутреннего get-а. Внутренний get, обращающийся к дереву отрезков, всегда (кроме случая в самом верху) считает максимум на префиксе, т.е. запрос зависит только от вершины v. Давайте хранить cash[v] (максимум на префиксе), calcTime[v] (время, когда мы считали этот максимум), и changeTime[tree[v]] (время, когда последний раз менялось соответствующее дерево отрезков), и, если changeTime[tree[v]] < calcTime[v], то не нужно считать еще раз, можно сразу вернуть cash[v].
Теперь время обработки одного запроса = (последний внутренний get) + (количество внутренних get-ов) +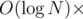 
{количество незакэшированных префиксов}. При этом все ранее незакэшированные префиксы закэшируются.
5) Вопросы
Вопрос #1: а не работает ли это амортизационно за ? (у меня строгого доказательства придумать не получилось).
Вопрос #2: идея, кажется, простая. Но я о ней узнал только сегодня. Кто-нибудь этим пользуется (на контестах, например)? Откуда это известно?
Вопрос #3: вы знаете другие способы заставить HLD работаеть за ?
Вопрос #4: может быть, я туплю, и задача на самом деле решается за на запрос, но проще (без HLD и Link-Cut)?
Конец
Ты еще забыл упомянуть, что бывают запросы не на префиксе, это происходит возле LCA(a, b) но такой запрос может быть лишь один. общий вклад в стоимость O(log(N)) поэтому забудем про него снова.
Рассмотрим такой пример: есть длинный ствол вниз, и от него на каждом уровне торчит по вершине в сторону (ветки). пройдемся запросами get по всем веткам. для дерева ствола все запросы закэшируются. Теперь изменим самую первую вершину ствола (и всегда будем менять только первую вершину, ибо это действие похерит всё закэшированное ранее).Изменение вершины ствола привело к тому, что к последующим запросам каждой ветки прибавиться O(log(длина ствола)). Это для иллюстрации, ведь понятно что в данном случае любой запрос разбивается всего на два запроса: один к стволу, а второй к дереву этой ветки из одной вершины. общая стоимость остаётся O(log(N)). Если бы ветки состояли не из одной вершины, а там висело что-то ветвистое, то это бы ничего не изменило т.к. соответствующий префикс ствола закешируется после запроса содержащего любую из вершин этой ветки. Итак change запрос вносит в общий вклад в худшем случае O(log(размер дерева на котором проведено изменение)) * (размер дерева на котором проведено изменение) но на самом деле вклад прибавляемый к в общему времени исполнения есть O(log(размер дерева на котором проведено изменение)) * (**количество различных веток**, к которым далее последуют get запросы). Блин, тут мне стало понятно, что ничего непонятно, подумаю и продолжу...
Продолжение
Если начинать с того, что у нас всё закэшировано (что требует непонятно сколько времени) то далее всё будет O(Q * Log(N)):
change запросы стоят O(Log(N))
get запросы стоят O(log(N)) * (1 + кол-во деревьев на пути, где до этого сбросили кэш change запросом)
Теперь запишем сумму всех проделанных действий, раскрывая скобки второго запроса. т.е. для запроса get получим:
(В квадратных скобках помечаю откуда эта стоимость.)
O(Log(N))[стоимость разбивания на цепи] + O(Log(N))[стоимость запроса к дереву отрезков, кэш которого сбил change запрос номер i1] + ... + O(Log(N))[стоимость запроса к дереву отрезков, кэш которого сбил change запрос номер iLogN]
В этой сумме все индексы сбивших кэш change запросов различны, и общая стоимость O(Q * Log(N))
Вроде упомянул... правда, как всегда кратко )
С этого нужно было начинать :) а то я, когда до конца дочитал, уже не понимал, к чему это.
Да мне вроде было понятно всё, когда начинал писать, а потом понял что обламался, поскольку букав много уже написал запостил. смотри продолжение, но оно тоже хреновое ибо непонятно как прийти к закешированному дереву.
не туда
Про продолжение:
Один change запрос сбрасывает кэш сразу для всего дерева, т.е. для многих вершин. И через каждую из этих вершин можно пустить get-запрос. Я не понял, где это учитывается. Наверное, это должно быть где-то в переходе от "все i различны" к O(Q * logN).
я тоже уже понял что вру. очевидно что i различны для одного запроса, но из этого ничего не следует.
пометим каждый прибавляемый логарифм индексами i и j. i — номер change запроса сбившего кеш, j номер get запроса. для одного конкретного j не будет двух слагаемых с одинаковым i. С другой стороны конкретный i встречается только у одного j. отсюда я каким-то магическим образом заключил что у нас O(Q) слагаемых, и спорол то что спорол.
Upd: конкретный i встречается только у одного j поддерева
Разве это так? У нас же i сбросило кэш у многих вершин.
Upd: конкретный i встречается только у одного j поддерева
поддерево — всмысле та часть дерева что идёт в ветку от ствола на котором был закэшированный запрос.
видимо в последней правке и заключалась магия.
Сообщение для идиотов, чтобы можно было побольше поминусовать.
Человек поставил интересный вопрос, и я над ним размышляю. Я ошибся в своих суждениях, бывает. Но возможно мои сообщения как-то помогут ему или другим участникам разговора найти решение. Что вы в этом находите раздражительным или негативным, тем что заставляет вас минусовать все мои сообщения я не понимаю.
Мысли — это хорошо.
Возможно, минусы значат, что оформленность и законченность мысли для кого-то важнее скорости ;-)
Теме 40 часов, мое первое сообщение — первое сообщение в теме, и оставлено менее 2 часов назад. Похоже на то, что я пытался написать что-попало, лишь бы быстрее остальных.
Вообще, если я правильно понимаю эту науку, то Link-Cut Tree -- это по сути как раз кеширование HLD. Мы храним все в Splay-деревьях, и как только "дотрагиваемся" до элемента, то делаем Splay на нем, что переносит его близко к корню.
Ну между Link-Cut Tree и HLD основная разница (когда нет link и cut, которых в HLВ и не может быть) в том, что в одном случае пути статичны, а в другом они меняются. Конечно в каком-то смысле это действительно кэширование, но в каком-то очень странном смысле.
Кстати, мы с Burunduk1 вроде поняли, что обычный HLD в log^2 не умеем-то валить (ну во всяком случае я). Какой будет худший тест?
Ну да, пути меняются, но я не согласен, что это кэширование в странном смысле. Давай рассмотрим ситуацию не примере Splay-дерева. Пусть мы ничего не добавляем и не удаляем, а только делаем запросы. Дерево будет меняться -- элементы, которые мы находим, переходят в корень. На самом деле, если подумать, то это очень естественная вещь. Это дает нам два очень естественных свойства:
ИМХО, эти свойства никоим образом не являются неестественными.
Хорошо, согласен. Но это кэширование не в том смысле, в котором имел ввиду Сережа.
Паша, ты не прав ;-)
Смотри почту внимательней. 1-й тест ты вчера запорол, про 2-й так ничего и не написал (письмо сегодня, 12:08 PM).
Тест, на котором HLD работает за Θ(log2N) :
Бинарное дерево. Сначала есть только корень. Идем сверху-вниз, слева-направо. Идем logN шагов. От каждой вершины откладываем влево N/2, N/4, N/8... вершин соответственно.
Теперь, если делать запрос от самой правой вершины, то нам последовательно будут попадаться деревья отрезков из 1, 2, ... N/4, N/2 вершин. Запрос на каждом работает за logN, если реализуем дерево отрезков сверху. Если реализуем снизу, то быстрее -- за log Len, где Len -- длина отрезка запроса (в данном случае Len = 1).
Тогда сделаем чуть умнее — N/3 влево, развилка, от нее N/3 влево, а справа крепится аналогичная конструкция с основанием N/9. Теперь время работы = log(N/3) + log(N/9) + log(N/27) + ... = Θ(log2N). Константа мала, но асимптотика на лицо ;-)
Link-Cut и HLD с кэшированием чем-то похожи...
Но, по-моему, это как сравнивать декартово дерево с деревом отрезков ;-) Да, дерево отрезков в целом бесполезно. Да, каждая вершина декартова дерева по неявному ключу -- отрезок массива. Но дерево отрезков таки короче пишется и имеет меньшую константу.
Excuse me for commenting in English, but my Russian is not so good.
About question 3: I think the following enhancement to the basic H-L decomposition should work for O(logn): In the H-L decomposition, for each heavy path, we build some kind of accumulative data structure (index, or segment tree), which answers the composition of element of a given interval in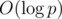
time, where p is the length of the path. A simple enhancement to this is to add to such an index tree an element, which will hold the composition of all of the elements in the interval, making the query O(1) on for the full interval. This just adds an additive constant to the update operation. Now, every (internal node — another descendant internal node) path in the tree is a path containing at most 
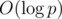light edges and 
heavy paths, but actually only the first and the last of the heavy paths could potentially be not the full heavy paths. For the internal paths, we could use this additional information, to answer the composition of all element along them in O(1). For the cornering heavy paths, we just will have to do at most another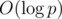 
queries, so the total query time should stay 
. But I may be missing something here...
Actually, not true.