byte_gambler's blog

SPOJ Fibosum
By byte_gambler, 11 years ago, In English

Can anyone help with this fibosum problem in SPOJ. I tried it with normal method by storing the fibonacci numbers in array and finding the sum. http://www.spoj.com/problems/FIBOSUM/

  • Vote: I like it
  • 0
  • Vote: I do not like it

Comments Comments (5)
| Write comment?
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Well, your method isn't normal because the constrains are too big.
I think this problem can be solved using binary exponentiation of a matrix.

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it +3 Vote: I do not like it

At first, sorry for my english.

Let 's call S(n) = FIB(1) + FIB(2) + ... + FIB(n)

It is easy to calculate S(n), DIY (Hint: try calculate S(1), S(2), S(3), S(4) by hand (or computer, whatever), you should find a very simple formula)

The rest is easy. O(lg (max(m, n))

→ Reply
»
11 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

It's clear that we only need the sum of the first n Fibonacci numbers. As we know that

with $F_0=F_1=1$, the sum of all Fibonacci numbers from 0-th to n-th will be just a geometric series:

where $E$ is the 2x2 unit matrix and division by matrix A - E can be replaced by multiplication by the inverse of that (non-singular) matrix, which is

so in this particular case (Fibonacci numbers),

and using modular exponentiation of matrices, the result can be computed in $O(\log{N})$ time.

Alternatively, you could use a modular inverse matrix: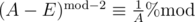 , it requires less knowledge about matrices.

→ Reply
»
11 years ago, # |
  Vote: I like it 0 Vote: I do not like it

There's a nice identity that you can prove by induction or by telescoping sums: F0 + F1 + ... + Fn = Fn + 2 - 1. This way, you only have to calculate two fibonacci numbers per query and this can be done with matrix exponentiation as everyone else said.

→ Reply