Can anyone help with this fibosum problem in SPOJ. I tried it with normal method by storing the fibonacci numbers in array and finding the sum. http://www.spoj.com/problems/FIBOSUM/
→ Обратите внимание
До соревнования
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
36:38:55
Зарегистрироваться »
CodeTON Round 9 (Div. 1 + Div. 2, Rated, Prizes!)
36:38:55
Зарегистрироваться »
*есть доп. регистрация
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
→ Найти пользователя
→ Прямой эфир
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 22.11.2024 04:56:05 (j2).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|










Well, your method isn't normal because the constrains are too big.
I think this problem can be solved using binary exponentiation of a matrix.
At first, sorry for my english.
Let 's call S(n) = FIB(1) + FIB(2) + ... + FIB(n)
It is easy to calculate S(n), DIY (Hint: try calculate S(1), S(2), S(3), S(4) by hand (or computer, whatever), you should find a very simple formula)
The rest is easy. O(lg (max(m, n))
If you lazy: http://www.wolframalpha.com/input/?i=Sum+Fib%28n%29
It's clear that we only need the sum of the first n Fibonacci numbers. As we know that
with $F_0=F_1=1$, the sum of all Fibonacci numbers from 0-th to n-th will be just a geometric series:
where $E$ is the 2x2 unit matrix and division by matrix A - E can be replaced by multiplication by the inverse of that (non-singular) matrix, which is
so in this particular case (Fibonacci numbers),
and using modular exponentiation of matrices, the result can be computed in $O(\log{N})$ time.
Alternatively, you could use a modular inverse matrix: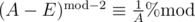 , it requires less knowledge about matrices.
, it requires less knowledge about matrices.
There's a nice identity that you can prove by induction or by telescoping sums: F0 + F1 + ... + Fn = Fn + 2 - 1. This way, you only have to calculate two fibonacci numbers per query and this can be done with matrix exponentiation as everyone else said.